
ทฤษฎีเซต : ทฤษฎีบทที่ 1 >>(กฎปฏิเสธสมมาตร) A=B ก็ต่อเมื่อ A⊆B และ B⊆A
ทฤษฎีบทนี้จะกล่าวว่า เซตสองเซตจะเท่ากันก็ต่อเมื่อทั้งสองเซตเป็นสับเซตซึ่งกันและกัน
ผู้เข้าชมรวม
1,296
ผู้เข้าชมเดือนนี้
3
ผู้เข้าชมรวม
1.29K
ข้อมูลเบื้องต้น
- สัจพจน์สับเซต
- นิยามสับเซต
- นิยามสับเซตแท้
- การพิสูจน์ทฤษฎีบทที่ 1
เนื้อเรื่อง
คืนค่าการตั้งค่าทั้งหมด
คุณแน่ใจว่าต้องการคืนค่าการตั้งค่าทั้งหมด ?
ลับมาพบันอีรั้แล้วรับับทฤษีเ
เรามาทบทวนันีว่าว่าอนที่แล้วเราไ้อะไรมาบ้า
----------[วามเิมอนที่แล้ว]----------
พิสูน์ : เว่า่าาเอเว่า
>>สัพน์ 1<<
: สัพน์เอ์เทนัน (Extension Axiom)
“ำหน A และ B เป็นเ เ A ะเท่าับเ B ็่อเมื่อทั้สอเมีสมาิเหมือนันทุัว”
>> สัพน์ 2<< : สัพน์เว่า (Empty
Set Axiom)
“เว่า เป็นเที่ไม่มีสมาิ”
>>นิยาม 1<< : เว่า
“ให้ A เป็นเใ ๆ เรีย A ว่าเว่า็่อเมื่อ A ไม่มีสมาิ”
สัพน์ หมายถึ้อวามที่เป็นริโยไม่้อมีารพิสูน์
นิยาม หมายถึ
้อวามที่ำัวามหมายอสิ่นั้น ๆ
เมื่อรั้ที่แล้วผมไ้อธิบายารเท่าันอเสอเว่า
A และ B ะเป็นเที่เท่าัน็่อเมื่อทั้สอเมีสมาิเหมือนันทุัว
แ่ราวนี้เราะมาอธิบายารเท่าันอเในอีรูปแบบหนึ่ นั่นือารนำ “สับเ” มาอธิบายนั่นเอ
น้อ ๆ ม.4
ะุ้น ๆ ว่าสับเืออะไร แ่ถ้าใรยัไม่เ้าใในเรื่อสับเ เี๋ยวผมะอธิบายให้
(มา ๆ มานั่ฟั)
ลอมอประเทศหนึ่ ๆ เป็นเ เ่น
ประเทศไทย็แล้วัน และ็มอรุเทพฯ เป็นเ ๆ หนึ่ เราบอว่ารุเทพฯ
อยู่ในประเทศไทย ึ่ทุนยอมรับ แ่ถ้าลอเปลี่ยนำพูให้เ้าับบรรยาาศแห่เ็ะเป็น
“รุเทพฯ เป็นสับเในประเทศไทย” นั่นืออาาบริเวในรุเทพฯ
ทั้หมนั้นเป็นบริเวอประเทศไทย้วย
ันั้น ถ้า A
เป็นสับเอ B แล้วะหมายถึสมาิทั้หมในเ
A เป็นสมาิอเ B ้วย
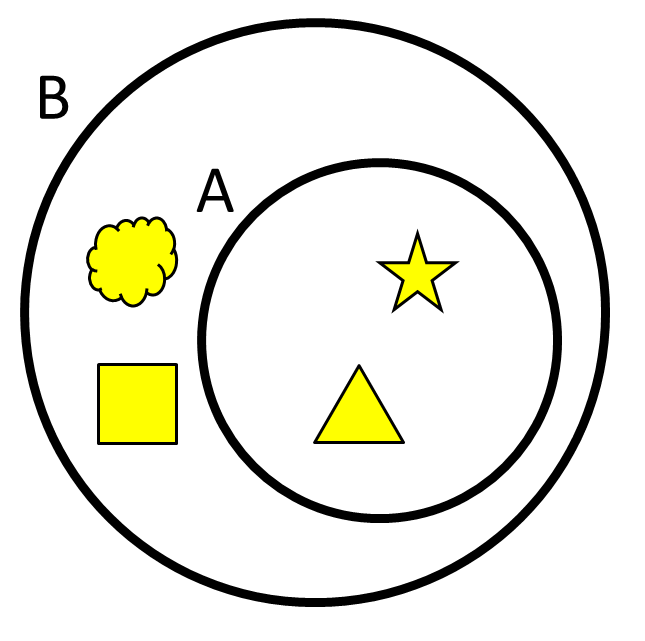
าภาพ้า้น ะเห็นว่า A
เป็นสับเอ B เนื่อาสมาิทั้หมในเ A
่า็เป็นสมาิในเ B ล่าวือ
A = {าว,
สามเหลี่ยม}
B = {าว,
สามเหลี่ยม, ้อนเม, สี่เหลี่ยม}
ะเห็นว่ามี าว ับ สามเหลี่ยม
ที่เป็นสมาิร่วมัน ทำให้ A เป็นสับเอเ
B นั่นเอ
โยสัลัษ์แทนำว่า “เป็นสับเอ”
ือ “
ทีนี้ ทฤษีบทนี้หมายวามว่าอะไร
หมายวามว่า(A
ับ B เป็นเนะ) ถ้า A=B แล้วเราะบอไ้ว่า A

A
VS.
B
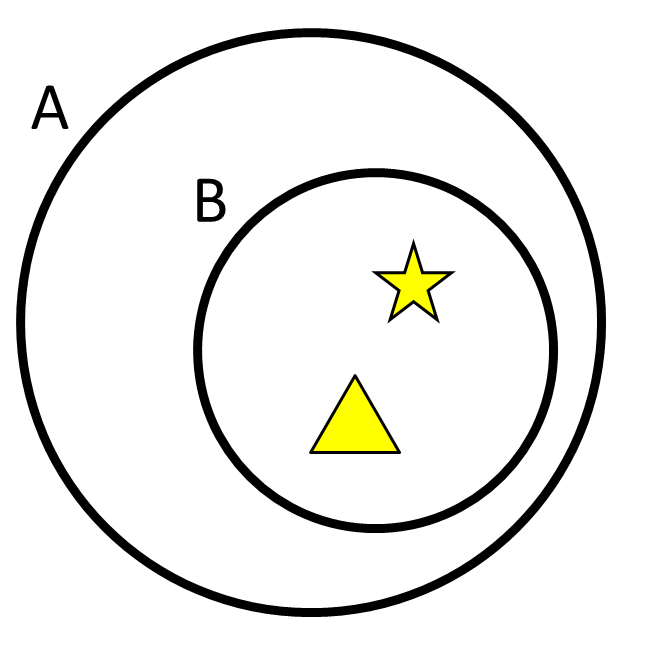
สอรูป้าบนนั้น ะเห็นว่าทั้สอเมีสมาิเหมือนัน
(มี าว ับ สามเหลี่ยม เป็นสมาินั่นเอ)
แ่ะเห็นว่าทั้สอเสามารถเป็นสับเอันและัน
นั่นือทั้สอเเป็นเเียวันนั่นเอ
นี่แหละ ือวามหมายอทฤษีบทนี้
ราวนี้ พี่ะเริ่มารพิสูน์แล้วนะ
แ่่อนอื่น พี่้อเปิไอเทม่อน ราวนี้พี่มีไอเทม 3
ิ้น เป็น ไอเทมสัพน์ 1 ิ้น
และเป็นไอเทมนิยาม 2 ิ้น
>>สัพน์ 3<< สัพน์สับเ (Subset
Axiom)
“สำหรับ A เป็นเใ ๆ มี B ึ่ x เป็นสมาิใ
ๆ ในเ B แล้ว x เป็นสมาิในเ A”เียนเป็นภาษารรศาสร์เป็น :
>>นิยาม 2<< สับเ (Subset)
“ำหนให้ A และ B เป็นเ ะเรียว่าเ B เป็นสับเอเ A ็่อเมื่อสมาิทุัวในเ B
เป็นสมาิในเ A แทน้วยสัลัษ์ B
>>นิยาม 3<< สับเแท้ (Proper Subset)
“ำหนให้ A และ B เป็นเ ะเรียว่าเ B เป็นสับเแท้อเ A ็ื่อเมื่อเ B เป็นสับเอเ A และ B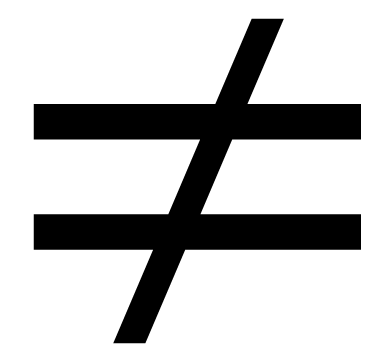

เมื่อเราเปิไอเทมเรียบร้อยแล้ว
เรามาเริ่มารพิสูน์ัน
Proof
: (ปิเสธสมมาร : The anti-symmetric law)
“ำหนให้ A
และ B เป็นเ ะไ้ A=B
็่อเมื่อ A

ารพิสูน์้อวามที่มีำว่า
“็่อเมื่อ” เราะ้อพิสูน์สอทาไปลับ
(แ่โีที่้อนี้เมื่อพิสูน์าไปแล้วไ้าลับเลย
เพราะสามารถเื่อมัน้วยเรื่อหมาย “็่อเมื่อ”)
าสัพน์เอ์เทนัน :
ำหน A และ B เป็นเ
เ A ะเท่าับเ B ็่อเมื่อทั้สอเมีสมาิเหมือนันทุัว
ให้ x เป็นสมาิึ่
แล้วระาย “็่อเมื่อ” ามสมบัิ
านิยามสับเ :
ำหนให้ A และ B เป็นเ
ะเรียว่าเ B เป็นสับเอเ A ็่อเมื่อสมาิทุัวในเ
B เป็นสมาิในเ A แทน้วยสัลัษ์ B
นั่นือ
เราสามารถสรุปไ้เลยว่า A=B ็่อเมื่อ A

ะเห็นว่าทฤษีบทนี้มีารนำรรศาสร์มา่วยในารพิสูน์
ทำให้ารพิสูน์มีวามัเน ไม่ำวม
ราวนี้มาถึาอน้อ ๆ แล้ว
พี่อยาให้น้อพิสูน์ว่า
“ำหนให้ A และ B
เป็นเ แสว่า ถ้า A=B แล้ว B=A”
(แล้วะมาเลยในทฤษีบทที่ 5
นะ ^^)
พบับใหม่อน่อไป
ผลงานอื่นๆ ของ ZigmaInfinity ดูทั้งหมด
ผลงานอื่นๆ ของ ZigmaInfinity








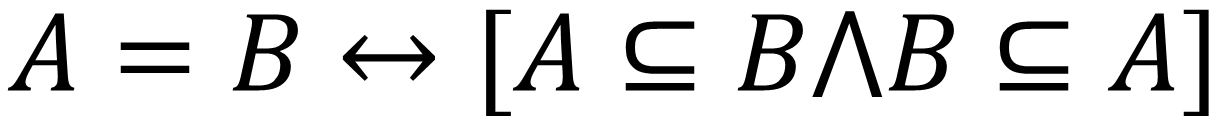
ความคิดเห็น