คืนค่าการตั้งค่าทั้งหมด
คุณแน่ใจว่าต้องการคืนค่าการตั้งค่าทั้งหมด ?
ลำดับตอนที่ #5 : เซตจำกัดและเซตอนันต์
เำัและเอนัน์ (Finite Set and Infinite Set)
1. เำั หมายถึเที่มีำนวนสมาิเท่าับำนวนเ็มบวใ ๆ หรือศูนย์ หรือเที่สามารถบอำนวนสมาิไ้ เ่น
A = {x | x เป็นเลโ}
A = {0, 1, 2, 3 ,4, 5, 6, 7, 8, 9}
A เป็นเำั เพราะบอสมาิไ้แน่นอนว่ามีสมาิ 10 ัว
2. เอนัน์ หมายถึเที่ไม่ใ่เำั หรือเที่ไม่สามารถบอำนวนสมาิไ้ เ่น
B = {1, 2, 3, …}
B เป็นเอนัน์ เพราะไม่สามารถบอำนวนสมาิไ้
3. เว่า (Null Set or Empty Set) หมายถึเที่มีำนวนสมาิเป็นศูนย์ เ่น
C = {x | x เป็นำนวนเ็มบวที่น้อยว่า -2}
C เป็นเว่า/เป็นเำั เพราะมีำนวนสมาิเป็น 0 สามารถเียนแทน้วย 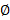
4. เอภพสัมพัทธ์ (Relative Universe) หมายถึเที่เป็นอบเอสมาิอเที่เรา้อารศึษา เ่น
U = {1, 2, 3, …, 9} แสว่าสมาิที่้อาระศึษาไ้แ่ 1, 2, 3, …, 9
หาเนั้นเป็นเอำนวน่า ๆ เราสามารถเียนเแบบบอเื่อนไโยระบุเอภพสัมพัทธ์ไ้ เ่น
D = {x | x ∈ N , x2 = 16}
E = {x | x ∈ I- , x2 = 16}
ะไ้ว่า D = { 4 } แ่ E = { -4 }
*** ถ้าไม่ไ้ำหนเอภพสัมพัทธ์ ให้ถือว่าเอภพสัมพัทธ์ือเอำนวนริ
F = {x | x2 = 16}
ะไ้ว่า F = { -4 , 4 }



ความคิดเห็น