ค่าเริ่มต้น
- เลื่อนอัตโนมัติ
- ฟอนต์ THSarabunNew
- ฟอนต์ Sarabun
- ฟอนต์ Mali
- ฟอนต์ Trirong
- ฟอนต์ Maitree
- ฟอนต์ Taviraj
- ฟอนต์ Kodchasan
- ฟอนต์ ChakraPetch
คืนค่าการตั้งค่าทั้งหมด
คุณแน่ใจว่าต้องการคืนค่าการตั้งค่าทั้งหมด ?
ลำดับตอนที่ #2 : สมดุลต่อการเคลื่อนที่
การเคลื่อนที่ของวัตถุแข็งแกร่งอาจแบ่งได้เป็น 2 แบบคือ
1. การเคลื่อนที่แบบเลื่อนที่ คือทุกส่วนเลื่อนไปในทางเดียวกัน เช่น การผลักไม้บรรทัดแล้วไม้บรรทัดเลื่อนไปข้างหน้าทิศเดียวกัน
2. การเคลื่อนที่แบบหมุน คือมีส่วนเป็นแกนหมุนและส่วนอื่นๆเคลื่อนที่หมุนรอบแกน เช่น การเคลื่อนที่ของพัดลม แต่วัตถุบ้างที่ก็เคลื่อนที่แบบหมุนและเลื่อนที่ไปพร้อมๆกัน เช่น การเคลื่อนที่ของลูกบอล
เมื่อพิจารณาการเคลื่อนที่เป็นหลักอาจแบ่งสมดุลของวัตถุได้ 3 ชนิด คือ
1. สมดุลต่อการเลื่อนที่ (Translational Equilibrium ) คือ วัตถุอยู่นิ่งหรือเคลื่อนที่ด้วยความเร็วคงตัว โดยไม่เปลี่ยนสภาพการเคลื่อนที่ตามกฎข้อที่ 1 ของนิวตัน จะมีค่าแรงลัพธ์หรือผลรวมของแรงลัพธ์ที่กระทำต่อวัตถุทั้งหมดเป็นศูนย์ หรือเขียนได้ว่า SF = 0
2. สมดุลต่อการหมุน ( Rotational Equilibrium ) คือสมดุลที่เกิดขึ้นในขณะที่วัตถุมีอัตราการหมุนคงตัว และไม่เปลี่ยนสภาพการหมุน
3. สมดุลสัมบูรณ์ของวัตถุ คือสภาพที่วัตถุนั้นเกิดสมดุลต่อการเลื่อนที่ (อยู่นิ่งหรือเคลื่อนที่ด้วยความเร็วคงที่)และ สมดุลต่อการหมุน(ไม่หมุน) ไปพร้อมๆกัน แรงต่างๆ ที่กระทำต่อวัตถุเป็นไปตามเงื่อนไข 2 ประการ คือ
1. แรงลัพธ์เป็นศูนย์ หรือผลรวมของแรงทุกแรงที่กระทำต่อวัตถุเป็นศูนย์ ( å F = 0 ) 2. ผลรวมของโมเมนต์ของแรงทุกแรงที่กระทำต่อวัตถุเป็นศูนย์ ( å M = 0 )
• สมดุลที่เกิดจากแรง 2 แรง •
เมื่อมีแรงกระทำต่อวัตถุ 2 แรงแล้ววัตถุสมดุลต่อการเคลื่อนที่( อยู่นิ่งหรือเคลื่อนที่ด้วยความเร็วคงตัว)ดังรูป
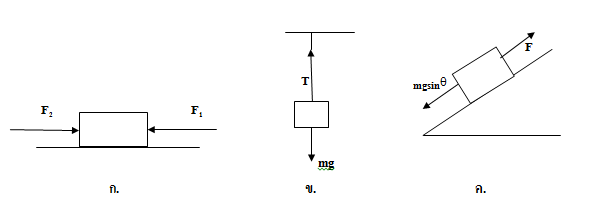
จากรูป ได้ว่าแรงทั้งสองต้องมีความสัมพันธ์กันดังนี้
1. แรงทั้งสองต้องมีขนาดเท่ากัน จากรูป (ก.) F1 = F2 (ข.) T = mg และ (ค.) F = mgsinq
2. แรงทั้งสองต้องมีทิศทางตรงกันข้าม และอยู่ในแนวเส้นตรงเดียวกัน
3. แรงลัพธ์ (SF = 0) ของแรงทั้งสองเท่ากับศูนย์
___________________________________________
• สมดุลของแรง 3 แรง •
เมื่อมีแรงกระทำต่อวัตถุ 3 แรง แล้ววัตถุสมดุลต่อการเคลื่อนที่( อยู่นิ่งหรือเคลื่อนที่ด้วยความเร็วคงตัว)

จากรูป ได้ว่าแรงทั้งสามต้องมีความสัมพันธ์กันดังนี้
1. แรงทั้งสามต้องพบกันที่จุดๆหนึ่งเท่านั้น หรือแรงทั้งสามขนานกันหมด
2. แรงทั้งสามต้องอยู่ในระนาบเดียวกันเท่านั้น
3. ผลรวมของแรงคู่ใดคู่หนึ่งต้องมีขนาดเท่ากับแรงที่สาม แต่มีทิศทางตรงกันข้าม
4. ถ้าเขียนผลรวมแรงทั้งสามจะได้ว่า
F1+F2+F3 = 0
หรือ F1+F2 = -F3
• สมดุลของแรงหลายแรง •
เมื่อมีแรงกระทำต่อวัตถุหลายแรง แล้ววัตถุสมดุลต่อการเคลื่อนที่(อยู่นิ่งหรือเคลื่อนที่ด้วยความเร็วคงตัว)
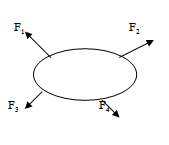
1. แรงเหล่านั้นไม่จำเป็นต้องพบกันที่จุดๆเดียวกัน เช่นดังรูป
2. แรงเหล่านั้นไม่จำเป็นต้องอยู่ในระนาบเดียวกันเท่านั้น เช่น
3. เมื่อเขียนสมการผลรวมของแรง จะได้ว่า
F1+F2+F3+…+Fn = 0
เมื่อวัตถุอยู่ในสภาพสมดุลต่อการเคลื่อนที่พบว่า SF = 0 และยังพบอีกว่าไม่ว่าจะหาผลรวมของแรงย่อยในทิศทางใดๆ ก็จะมีแรงลัพธ์ในแนวนั้นๆ เท่ากับศูนย์ด้วย
ดังนั้นอาจเขียนได้ว่าเมื่อวัตถุสมดุลต่อการเคลื่อนที่
1. SFX = 0 จะได้ว่า ผลรวมของแรงทางขวา = ผลรวมของแรงทางซ้าย
2. SFy = 0 จะได้ว่า ผลรวมของแรงพุ่งขึ้น = ผลรวมของแรงพุ่งลง
# หมายเหตุ ในการแก้ปัญหาสมดุลต่อการเคลื่อนที่ อาจใช้แกนตั้งฉาก 2 แกนในแนวอื่นๆก็ได้ผลเหมือนกันไม่จำเป็นต้องเป็นแกน x , y เสมอไป
จากรูปข้างต้น จะได้ความสัมพันธ์ของแรงเมื่อวัตถอยู่ในสภาพสมดุลต่อการเคลื่อนที่ว่า
1. SFX = 0 ได้ว่า F1cosq + F4 sing = F2sinb + F3cosa
2. SFy = 0 ได้ว่า F1sinq + F2cosb = F3sina + F4 cosg
ซึ่งจากความรู้เรื่องสมดุลต่อการเคลื่อนที่ เราอาจนำไปใช้แก้ปัญหาโจทย์หาแรงที่ไม่ทราบค่าได้
ก่อนจากกัน *










ความคิดเห็น