PHYSICS:สมดุลกล

ลำดับตอนที่ #6 : สมดุลกลและสภาพยืดหยุ่น

สมดุลกลและสภาพยืดหยุ่น

 

สภาพยืดหยุ่น (elasticity) สมบัติ ของวัตถุที่เปลี่ยนแปลงรูปร่างได้เมื่อมีแรงกระทำ และจะกลับคืนสู่รูปร่างเดิมได้เมื่อหยุดออกแรงกระทำต่อวัตถุนั้น ตัวอย่างวัสดุที่มีสภาพยืดหยุ่น เช่น ฟองน้ำ 

 

           สมบัติ สภาพยืดหยุ่นของวัสดุ มีประโยชน์ในงานทางช่างและทางอุตสาหกรรมเป็นอย่างยิ่ง เช่น ในการเลือกวัสดุเพื่อใช้เป็นโครงสร้างอาคารสะพาน หรือชิ้นส่วนของเครื่องกล วิศวกรหรือผู้ออกแบบจะต้องพิจารณาสมบัติสภาพยืดหยุ่นของวัสดุที่จะนำมาใช้ ประโยชน์ให้เหมาะสมกับงาน วัสดุหลายชนิดมีทั้งสภาพยืดหยุ่นและสภาพพลาสติกในตัวเอง โดยมีสภาพยืดหยุ่นเมื่อแรงกระทำน้อย ๆ และมีสภาพพลาสติกเมื่อมีแรงกระทำมาก ๆ 

 

            สภาพยืดหยุ่นของของแข็ง   เป็นสมบัติของของแข็งที่มีการเปลี่ยนแปลงรูปร่างเมื่อมีแรงมากระทำ  แบ่งออกเป็น 2 ประเภท  คือ

 

                1.  สภาพยืดหยุ่น (elasticity)  คือ สมบัติของวัสดุที่มีการเปลี่ยนแปลงรูปร่าง  เมื่อมีแรงมากระทำและสามารถคืนตัวกลับสู่รูปร่างเดิมเมื่อหยุดออกแรงกระทำ    A

 

                2. สภาพพลาสติก  (plasticity) คือ กรณีวัสดุเปลี่ยนรูปร่างไปอย่างถาวร  โดยผิววัสดุไม่มีการฉีกขาดหรือแตกหัก 

 

            จากการดึงสปริงให้ยืดออก จะพบว่ากราฟระหว่างขนาดของแรงดึงกับความยาวที่สปริงยืดออก จะมีลักษณะดังรูป 

 

 

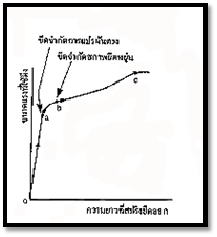
- จุด a  คือ ขีดจำกัดการแปรผันตรง (Proportional limit) ซึ่งเป็นตำแหน่งสุดท้ายที่ความยาวสปริงยืดออก แปรผันตรงกับขนาดของแรงดึง

- จุด b  คือ ขีดจำกัดสภาพยืดหยุ่น (Elastic limit) ซึ่งเป็นตำแหน่งสุดท้ายที่สปริงยืดออกแล้วกลับสู่สภาพเดิม แต่แรงดึงไม่แปรผันตรงกับระยะยืด

- จุด C  คือ จุดแตกหัก (Breaking point) หมายถึงตั้งแต่จุด b เป็นต้นไป ถ้าดึงต่อไปก็ถึงจุด c ซึ่งเป็นจุดที่เส้นวัสดุขาด

 

 

 

จากความรู้เรื่องสภาพยืดหยุ่นของวัตถุ  ทำให้ทราบว่า เมื่อมีแรงมากระทำกับวัตถุ พบว่ารูปร่างของวัตถุจะเปลี่ยนแปลงไป ตามทิศทางของแรงที่กระทำ โดยวัตถุเหล่านั้นจะประพฤติตามกฎของฮุก ถ้าแรงที่กระทำมีขนาดไม่มากเกินไป โดยแรงมีขนาดน้อยกว่า ขีดจำกัดสภาพยืดหยุ่น เช่น ลวด ,โลหะ , แก้ว , พลาสติก เป็นต้น  แต่มีวัตถุบางชนิดที่ไม่เป็นไปตามกฎของฮุก เช่น ดินน้ำมัน , หมากฝรั่ง เพราะเมื่อมีแรงกระทำเพียงเล็กน้อยรูปร่างจะเปลี่ยนไปอย่างถาวร  

 

โดยทั่วไปแล้วแรงที่กระทำต่อวัตถุมีผลทำให้วัตถุมีรูปร่างเปลี่ยนไป มี 3 แบบ ได้แก่

 

1. แรงดึง (tensile  forces) เป็นแรงที่กระทำต่อวัตถุ  มีผลทำให้ความยาวของวัตถุเพิ่มขึ้น

 

2. แรงอัด (forces  of compression) เป็นแรงที่กระทำต่อวัตถุ  มีผลทำให้ความยาวของวัตถุลดลง

 

3. แรงเฉือน (shear  forces) เป็นแรงที่กระทำบนผิววัตถุ มีผลทำให้ผิววัตถุเลื่อนไปหรือรูปรางวัตถุบิดรูปร่างไปจากเดิม ตามแนวยาว แรงที่กระทำนี้เรียกว่า แรงบิด (forces  of  torsion) ซึ่งเป็นแรงเฉือนชนิดหนึ่ง

 

♠-----------------------------------------------♠

 

ความเค้น ( stress )

 

ตามความเป็นจริงความเค้นหมายถึง แรงต้านทานภายในเนื้อวัสดุที่มีต่อแรงภายนอกที่มากระทำต่อหนึ่งหน่วยพื้นที่ แต่เนื่องจากความไม่เหมาะสมทางปฏิบัติ และความยากในการวัดหาค่านี้ เราจึงมักจะพูดถึงความเค้นในรูปของแรงภายนอกที่มากระทำต่อหนึ่งหน่วยพื้นที่ ด้วยเหตุผลที่ว่า แรงกระทำภายนอกมีความสมดุลกับแรงต้านทานภายใน การหาค่าความเค้นสามารถเขียนเป็นสมการได้ดังนี้คือ

 

เมื่อออกแรงกระทำต่อวัตถุ อัตราส่วนระหว่างแรงกระทำต่อพื้นที่ เรียกว่า ความเค้น เป็นปริมาณสเกลาร์ โดยทั่วไปความเค้นมี 2 ชนิด ได้แก่ ความเค้นตามยาวและความเค้นเฉือน

 

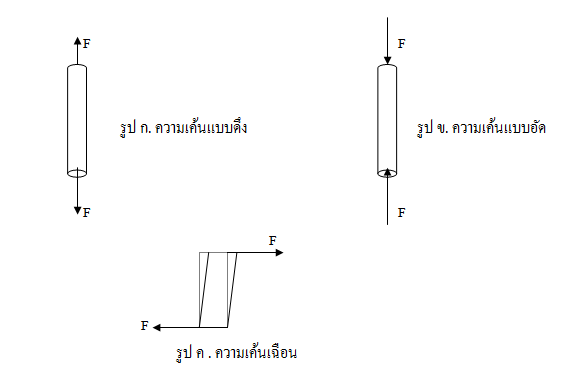
ความเค้นตามยาว (longitudinal  stress) แบ่งได้ 2 ชนิด คือ ความเค้นแบบดึง (tensile  stress) ซึ่งแรง F กระทำต่อวัตถุในลักษณะดึงให้ยืดออก   กับ ความเค้นแบบอัด ( compression  stress ) ซึ่งแรง F  กระทำต่อวัตถุในลักษณะอัดให้หดสั้นลง   

 

ส่วน ความเค้นเฉือน (shear  stress )  นั้น แรง F ที่กระทำต่อวัตถุจะทำให้วัตถุบิดเบือนรูปร่างไปจากเดิม

 

♠-----------------------------------------------♠

 

ความเครียด (Stain) 

 

เป็นความเครียดที่ปรากฏภายใต้แรงที่มากระทำต่อเนื้อของวัสดุ จนวัสดุเกิดรับแรงนั้นไว้ไม่ไหว ทำให้เกิดการเปลี่ยนแปลงขนาดและรูปร่างไปในทิศทางของแรงที่มากระทำ เช่น เกิดการยืดตัวออก (Elongation) หรือหดตัวเข้า (Contraction)โดยแบ่งชนิดของความเครียดได้เป็นดังนี้ คือ 

 

         1.Tensile Stain หมายถึง ความเครียดแรงดึงที่เกิดจาก Tensile Force ที่มากระทำต่อชิ้นงาน 

 

         2.Compressive Stain หมายถึงความเครียดแรงกด หรือ ความเครียดแรงอัด

 

         3.Shear Stain หมายถึงความเครียดแรงเฉือน เป็นความเครียดที่เกิดจาก Shear Force 

 

♠-----------------------------------------------♠

 

มอดูลัสของยัง (Young's modulus) 

 

หรือ มอดูลัสของสภาพยืดหยุ่น (modulus of elasticity หรือ elastic modulus) เป็นค่าบอกระดับความแข็งแกร่งของวัสดุ ค่ามอดูลัสของยังหาจาก ค่าลิมิดของอัตราการเปลี่ยนแปลงของความเค้น( stress ) ต่อ ความเครียด ( strain ) ที่ ค่าความเค้นน้อยสามารถหาจากความชัน ของ กราฟความสัมพันธ์ ความเค้น-ความเครียดที่ได้จาก การทดลองดึง ค่ามอดูลัสของยัง ตั้งชื่อตาม ชาวอังกฤษ โทมัส ยัง ซึ่งเป็นทั้งนักฟิสิกส์ แพทย์ แพทย์นรีเวช และผู้ที่ศึกษาวิชาเกี่ยวกับวัฒนธรรมและวัตถุโบราณของอียิปต์

 

           หน่วย SI ของมอดูลัสของสภาพยืดหยุ่น คือ ปาสกาล (Pascal)ค่า มอดูลัสของยัง นั้นมีประโยชน์ใช้ในการคำนวณพฤติกรรมในการรับแรงของวัสดุ ตัวอย่างเช่น สามารถใช้ในการคาดคะเน ความยืดของลวดในขณะรับแรงดึง หรือคำนวณระดับแรงดันที่กดลงบนแท่งวัสดุ แล้วทำให้แท่งวัสดุยวบหักลง ในการคำนวณจริงอาจมีค่าอื่นๆ เกี่ยวข้องด้วย เช่น มอดูลัสของแรงเฉือน (shear modulus) ความหนาแน่น

          

การคำนวณ มอดูลัสของสภาพยืดหยุ่น หาได้จากการหาร ค่าความเค้น ด้วย ค่าความเครียด 

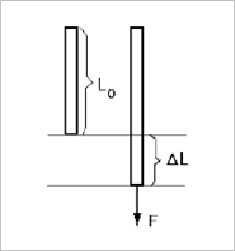
Y = ความเค้น/ความเครียด = σ/ε = (F ÷A)/(∆L ÷L) = (F.L)/(A.∆L )

 

:) Shalunla