ลำดับตอนที่ #28
คืนค่าการตั้งค่าทั้งหมด
คุณแน่ใจว่าต้องการคืนค่าการตั้งค่าทั้งหมด ?
ลำดับตอนที่ #28 : Classical Mechanics
ลศาสร์ั้เิมหรือลศาสร์ลาสสิ
อธิบายถึารเลื่อนที่อวัถุั้แ่วัถุบนโลถึวัถุทาาราศาสร์ ลศาสร์สามารถบอผลลัพธ์ไ้อย่าแม่นยำและเป็นหนึ่ในวิาที่เ่าแ่ที่สุในวิาวิทยาศาสร์และเทโนโลยี.
ลศาสร์ั้เิมหรือลศาสร์ลาสสิ (Classical Mechanics) ไ้รับารพันาโยนัิ นัทลอ นัประิษ์ และนัวิทยาศาสร์หลายๆท่าน หลัอานัและโมเมน์ (Moment) เป็นที่รู้และประยุ์ใ้ันอย่าแพร่หลายมานานนับพันปี ั้แ่สมัยออาร์ีมีิส (Archimedes) หลัอแรและารผ่อนแรเป็นสิ่ที่รู้และเ้าใเป็นอย่าีั้แ่สมัยอียิป์โบรา ึ่ถูนำมาใ้ในาร่อสร้าปิรามิอันยิ่ให่ อย่าไร็ี ุที่นับเป็นุเริ่ม้นอย่าเป็นทาารอลศาสร์ลาสสิือเมื่อ ไอแ นิวัน นัปรัาธรรมาิ (Natural Philosopher) าวอัฤษ ประาศารเลื่อนที่สาม้อในปีริส์ศัรา 1687 เป็นผลานอันลือเลื่อ ในหนัสือ พรินสิเปีย(Philosophiae Naturalis Principia Mathematica) นิวันประสบวามสำเร็ในารบรรยายารเลื่อนที่อทั้วาว (celestial motion)และอวัถุบนผิวโล (terrestrial motion) ไ้อย่าแม่นยำอย่าไม่เยมีมา่อน โยารเสนอ แห่วามโน้มถ่วสาล(universal law of gravitation) นิวันไ้พันาิศาสร์สาาแลูลัส (Calculus)เพื่อใ้ในารำนวารเลื่อนที่อวาวอันับ้อน นิวันสามารถแสให้เห็นว่า ำลัสอผผัน (Inverse square law)แห่วามโน้มถ่วอเา ำหนให้ทาโรอาวเราะห์รอบวอาทิย์เป็นรูปวลม วรี พาราโบลาและไฮเปอร์โบลา าวเราะห์ส่วนให่มีวโรเป็นวรี าวเราะห์น้อยและาวหามีทั้ที่โรเป็นวรี พาราโบลาและไฮเปอร์โบลา โยารสัเและเ็บ้อมูลอวัถุบนฟาฟ้า เราสามารถใ้อนิวันทำนายวโรในอีและอนาอวัถุเหล่านั้นไ้อย่าแม่นยำ
ารเลื่อนที่อนิวัน (Newton’s laws of motion)
เป็นราานิาพื้นานเี่ยวับารเลื่อนที่อวัถุภายใ้แรที่ระทำ (ว่า้วยารเลื่อนที่3 ้ออนิวัน) และทฤษีวามโน้มถ่วที่อธิบายว่าแรึ่ึูให้ผลแอปเปิลา้นสู่พื้น เป็นแรนิเียวับที่วบุมารโรรอบโลอวันทร์ นิวันไ้ศึษาารเลื่อนที่อวัถุและไ้เสนอารเลื่อนที่สาม้อ ารเลื่อนที่ทั้สาม้อไ้นำเสนออยู่ในหนัสือ Principia ารเลื่อนที่อนิวัน (Newton’s laws of motion) สำหรับวัถุ เป็นายภาพ(physical laws) ึ่เป็นที่เี่ยวับพฤิรรมอสสารที่เป็นริอยู่เสมออย่าไม่เปลี่ยนแปล โยเราไม่สามารถะวบุม ัแปล หรือแ้ไแห่วามริไ้[
ารเลื่อนที่้อ 1 อนิวัน (Newton’s first law of motion) หรืออวามเื่อย ล่าวว่า“วัถุะรัษาสภาวะอยู่นิ่หรือสภาวะเลื่อนที่อย่าสม่ำเสมอในแนวเส้นร นอามีแรลัพธ์ึ่มี่าไม่เป็นศูนย์มาระทำ”[6]ือ ถ้าวัถุอยู่นิ่็ยัอยู่นิ่เหมือนเิม และถ้าวัถุเิารเลื่อนที่็ะเลื่อนที่เป็นเส้นร วามเร็วที่ หรือวามเร่ะเป็นศูนย์ ึ่รีแระเรียว่า วัถุอยู่ในสภาวะสมุลสถิ (static equilibrium) และอีรีหลัะเรียว่า วัถุอยู่ในสภาวะสมุลลน์ (kinetic equilibrium) [7]มีสมารเป็นันี้ ∑F=0 Fือ แรลัพธ์ทั้มที่ระทำับวัถุ
ารเลื่อนที่้อ 2 อนิวัน (Newton’s second law of motion) บาทีเรียว่า วามเร่ ล่าวว่า“วามเร่ออนุภาเป็นปิภาโยรับแรลัพธ์ที่ระทำ่ออนุภา โยมีทิศทาเียวันและเป็นปิภาผผันับมวลออนุภา” [8]ันั้น อัราส่วนอแรับวามเร่ะเป็น่าที่ ึ่รับมวลอวัถุ เียนเป็นวามสัมพันธ์ไ้ันี้ ∑F = ma
F ือ แรลัพธ์ที่ระทำับวัถุ มีหน่วยเป็นนิวัน (N)
m ือ มวลอวัถุ มีหน่วยเป็นิโลรัม (kg)
a ือ วามเร่มีหน่วยเป็นเมร่อวินาที2 (m/s2)
ถ้าแรลัพธ์ (F) ระทำับวัถุอันหนึ่ ะทำให้วัถุมีวามเร่ (a) ในทิศทาเียวันับทิศทาอแร ึ่แรลัพธ์ (F) ที่ระทำับวัถุ ะเท่าับผลูระหว่ามวล (m) และวามเร่ (a) อวัถุ ะสรุปไ้ว่า “แรลัพธ์ที่ที่ระทำับวัถุ ึ่มีมวลที่ วัถุนั้นะมีวามเร่ที่ในทิศทาอแรที่ระทำนั้น”[9]
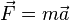
ารเลื่อนที่้อ 3 อนิวัน (Newton’s third law of motion) ล่าวว่า“ทุแริริยา (action) ย่อมมีแรปิิริยา (reation) ึ่มีนาเท่าัน แ่มีทิศร้ามันเสมอ”[10]้อนี้เรียว่า อิริยาและปิิริยา (Law of action and reaction) แริริยาและแรปิิริยา หมายถึ แรระทำและแรระทำอบ โยเป็นแรึ่ระทำ่อมวลที่่าันและเิึ้นพร้อมันเป็นู่เสมอ โยที่มวลอาไม่สัมผัสันและถือว่าแรหนึ่แรใเป็นแริริยาและแรปิิริยา็ไ้[11] เียนเป็นวามสัมพันธ์ไ้ันี้ FA = -FR
Domain of validity for Classical Mechanics
อบเอลศาสร์ลาสสิ
เก็บเข้าคอลเล็กชัน
ความคิดเห็น