[ NotebooK ] บันทึกการเรียน

ลำดับตอนที่ #6 : ภาคตัดกรวย

---------------------------------------

ภาคตัดกรวย  เป็นเส้นโค้งที่เกิดจากการตัดกรวยวงกลมด้วยระบาบต่างๆ
เกิดเป็น วงกลม วงรี พาราโบลา ไฮเปอร์โบลา

วงกลม	เกิดขึ้นจากการตัดกรวยกลมตรงด้วยระนาบที่ตั้งฉากกับแกนของกรวย
พาราโบลา	เกิดขึ้นจากการตัดกรวยกลมตรงด้วยระนาบที่ขนานกับเส้นประกอบรูปกรวย
วงรี	เกิดขึ้นจากการตัดกรวยกลมตรงด้วยระนาบที่ตัดกรวยเพียงส่วนเดียวโดยที่ระนาบนั้นไม่ขนาน กับเส้นประกอบรูปกรวยและไม่ตั้งฉากกับแกนของกรวย
ไฮเพอร์โบลา	เกิดขึ้นจากการตัดกรวยกลมตรงด้วยระนาบที่ขนานกับแกนของกรวยและตัดทั้งสองส่วนของกรวย

http://www.schoolptk.ac.th/~preecha/cone_history.htm

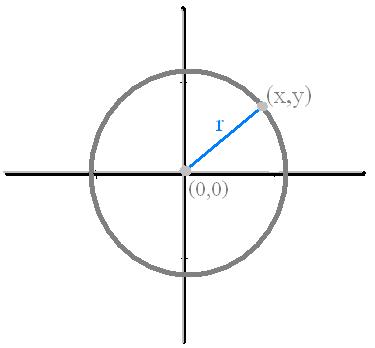
นิยามของวงกลม  คือเซตของทุกจุดบนระนาบซึ่งห่างจากจุดคงตัวระยะเท่ากัน

จุดคงตัวคือจุดศูนย์กลาง (h,k)
ระยะห่างจากจุดถุงจุดคงตัวคือรัศมี (r)
จุดบนระราบคือจุด (x,y)

จุดศูนย์กลางอยู่ที่จุดกำเนิด หรืจุด(0,0)  มีสูตรคือ   
                                                  
x²  +  y²  =  r² 





    

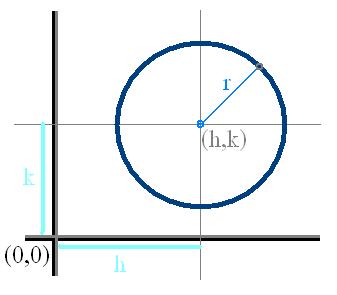
จุดศุนย์กลางอยู่ที่จุด (h,k)  มีสูตรคือ

สูตรมาตรฐานวงกลม (x – h)² + (y – k)² = r² 

สูตรทั่วไป             x² + y² + Dx + Ey + F = 0



หา (h,k) ได้จากสูตร 

 (h,k) =  

หารัศมีได้จากสูตร
 

                                              r  =

นิยามวงรี คือ เซตของจุดทุกจุดบนระนาบซึ่งผลบวกของระยะทางจากจุดใด ๆ ในเซตนี้ไปยังจุดคงที่ 2 จุด มีค่าคงตัว โดยค่าคงตัวนั้นมากกว่าระยะห่างระหว่างจุดคงที่ทั้งสอง

ผลบวกระยะทางระหว่างจุดบนวงรีไปยัง 
โฟกัส(F)ทั้งสอง  =  2a

 

community.thaiware.com/.../t345601.html

     

  แกนเอกของวงรีคือแกนที่ยาว   
 ส่วนแกนโทนั้นสั้นกว่าแกนเอก

แกนเอกยาว 2a และแกนโทยาว 2b

a คือระยะจากจุดศูนย์กลาง ถึงจุดยอด หรือ vertex (V)

b คือระยะจากจุดศูนย์กลาง ถึงจุด B

c คือระยะจากจุดศูนย์กลาง ถึง จุดโฟกัส (F)

เปรียบเทียบได้    a > b > 0  และ   a > c > 0

มีความสัมพันธ์คือ      a2 = b2 + c2

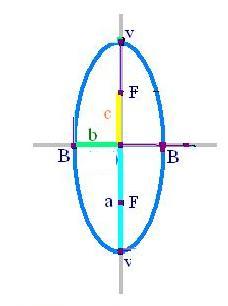
วงรีที่มีแกนเอกขนานกับแกน y

สมการ 
จุดศูนย์กลาง (h,k)

จุดโฟกัส (h,k-c) และ (h,k+c)

จุดยอด (h,k-a) และ (h,k+a)

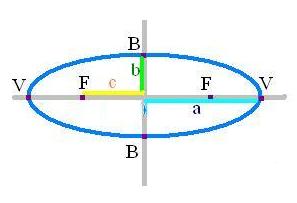
วงรีที่มีแกนขนานกับแกน x

สมการ

จุดศูนย์กลาง (h,k)

จุดโฟกัส (h – c,k) และ (h + c,k)

จุดยอด (h – a,k) และ (h + a,k)

 

Latus rectum ของวงรี คือ ส่วนของเส้นตรงที่มีจุดปลายอยู่บนวงรี และตั้งฉากกับแกนเอกที่จุดโฟกัส ซึ่งมีความยาว 

eccentricity

  ของวงรี เป็นตัวเลขที่บอกว่างวรีนี้นรีมากน้อยเพียงใด โดย    และ 0 < e < 1  
ถ้า e เข้าใกล้ 0 วงรีจะใกล้เคียงกับวงกลม แต่ถ้า e เข้าใกล้ 1 วงรีจะรีมาก 

ent2you.com/knowledge/1MATH/conic1.htm

 

www.mps.ac.th/match-rasamee/para.htm

บทนิยาม : พาราโบลาคือเซตของจุดทุกจุดบนระนาบ ซึ่งอยู่ห่างจากเส้นตรงที่ตรึงอยู่กับที่และจุดคงเป็นระยะทางเท่ากัน

เส้นตรงนั้นคือ เส้นไดเรกตริกซ์
จุดนั้นคือจุดโฟกัส

 พาราโบลาที่มีจุดยอดอยู่ที่ (0,0) 
สมการของพาราโบลาที่มีจุดยอด อยู่ที่ (0,0) แกนของพาราโบลา คือแกน x หรือ แกน y ซึ่งสามารถ แบ่งออกได้เป็น 4 ลักษณะ ดังนี้


 แกนของพาราโบลาคือแกน x และ โฟกัสอยู่ที่ (c,o) เมื่อ c > o
ไดเรกตริกซ์ คือ เส้นตรง x = c 
กราฟของพาราโบลาตะแคงขวา หรือ เปิดขวา

y² = 4cx 
y² = 4cx

ให้ P(x,y) เป็นจุดใดๆ บนพาราโบลา
PR = PQ
=



ข. แกนของพาราโบลาคือแกน x และโฟกัสอยู่ที่ (-c,0) เมื่อ c < 0
ไดเรกตริกซ์ คือ เส้นตรง x = -c 
กราฟของพาราโบลาเปิดซ้าย หรือตะแคงซ้าย

y² = -4cx 

ค. แกนของพาราโบลาคือแกน y และโฟกัสอยู่ที่ (0,c) เมื่อ c > 0
ไดเรกตริกซ์ คือเส้นตรง y = c
 กราฟของพาราโบลาจะหงาย

x² = 4cy

ง. แกนของพาราโบลาคือแกน y และโฟกัสอยู่ที่ (0,-c) เมื่อ c < 0
ไดเรกตริกซ์ คือ เส้นตรง y = -c 
กราฟของพาราโบลาจะคว่ำ
x² = -4cy

สมการของพาราโบลาที่จุดยอดที่จุด (h,k) 
และมีแกนขนานกับ แกน x หรือแกน y

แกนของพาราโบลาขนานแกน x และ โฟกัสอยู่ที่ (h + c,k) เมื่อ c > o
ไดเรกตริกซ์ คือ เส้นตรง x =  h - c
กราฟของพาราโบลาตะแคงขวา หรือ เปิดขวา

(y - k)² = 4c(x - h)





แกนของพาราโบลาขนานแกน x และ โฟกัสอยู่ที่ (h - c ,k) เมื่อ c < o
ไดเรกตริกซ์ คือ เส้นตรง x =  h + c
กราฟของพาราโบลาตะแคงขวา หรือ เปิดขวา

(y - k)² = - 4c(x - h)






แกนของพาราโบลาขนานแกน y และ โฟกัสอยู่ที่ (h ,k + c) เมื่อ c > o
ไดเรกตริกซ์ คือ เส้นตรง y =  k - c
กราฟของพาราโบลาหงาย

(x - h)² = 4c(y - k)







แกนของพาราโบลาขนานแกน y และ โฟกัสอยู่ที่ (h ,k - c) เมื่อ c < o
ไดเรกตริกซ์ คือ เส้นตรง y =  k + c
กราฟของพาราโบลาคว่ำ

(x - h)² = - 4c(y - k)









สรุปคือ 

ถ้า c > 0    กราจะหงาย หรือ ตะแขงขวา(เปิดขวา)
ถ้า c < 0  กราฟจะคว่ำ หรือ ตะเเคงซ้าย(เปิดซ้าย) 

เส้นลาตัสเลกตัม ( ลากผ่านF ) = l4cl

สมการพาราโบลา เส้นไดเรกตริกซ์ขนานแกนใด แกนั้นจะขึ้นก่อน

www.mps.ac.th/match-rasamee/hyper.htm

บทนิยาม ไฮเพอร์โบลา คือเซตของจุดทุกจุดในระนาบ ซึ่งผลต่างของระยะห่างจากจุดใดๆ ในเซตนี้ไปยังจุดคงที่สองจุดบนระนาบมีค่าคงตัว ซึ่งมากกว่าศูนย์ แต่น้อยกว่าระยะห่างระหว่างจุดคงที่


ส่วนประกอบที่สำคัญของไฮเพอร์โบลา

 จุดศูนย์กลางของไฮเพอร์โบลา คือจุดกึ่งกลางระหว่างโฟกัสทั้งสอง
ให้ c เท่ากับระยะห่างระหว่างจุดศูนย์กลางและโฟกัส

จุดยอดของไฮเพอร์โบลา คือจุดที่เส้นโค้งไฮเพอร์โบลาตัดกับ จุดยอดของไฮเพอร์โบลาจะมี 2 จุด แต่ละจุดจะอยู่ห่างจากจุดศูนย์กลางเท่ากัน
ให้ a เท่ากับระยะห่างระหว่างจุดศูนย์กลางและจุดยอด


แกนตามขวาง (transverse axis) ของไฮเพอร์โบลา คือส่วนของเส้นตรงที่เชื่อมระหว่างจุดยอดทั้งสองของไฮเพอร์โบลา
แกนตามขวางของไฮเพอร์โบลา คือ

แกนสังยุค (conjugate axis) ของไฮเพอร์โบลา คือส่วนของเส้นตรง ซึ่งแบ่งครึ่งและตั้งฉากกับแกนตามขวางของไฮเพอร์โบลา

 เส้นกำกับ (asypmptote) ของไฮเพอร์โบลา สร้างรูปสี่เหลี่ยมมุมฉาก โดยการลากเส้นให้ผ่านจุดยอดและลากเส้นให้ผ่านจุดปลายแกนสังยุค แล้วเส้นตรงที่อยู่ในแนวเส้นทแยงมุมของรูปสี่เหลี่ยมมีทั้งสองเส้นเรียกว่า เส้นกำกับของ ไฮเพอร์โบลา
เส้นกำกับจะช่วย ให้เขียนกราฟได้ง่ายและถูกต้องยิ่งขึ้น กล่าวคือ ไฮเพอร์โบลาจะผ่านจุดยอด เส้นโค้งของกราฟไฮเพอร์โบลา จะโค้งหาเส้นกำกับทีละน้อยๆ แต่จะไม่ตัดหรือทับเส้นกำกับ

สรุป ส่วนประกอบสำคัญๆ

1. แกนตามขวาง ยาว 2a

2. แกนสังยุค ยาว 2b

3. จุดตัดแกน V(h,k)

4. จุดโฟกัส 2 จุด (ระยะห่างโฟกัส 2c)

5. เส้นกำกับสองเส้น

6. จุดยอดไฮเพอร์โบลา 2 จุด (A และ A' )

7. ความสัมพันธ์ของ a b และ c คือ c² = a² + b² 

8.  c > a > 0  and  c > b > 0

9. แกนตามขวางจะคล้ายกับแกนเอก และแกนสังยุคจะคล้ายกับแกนโทของวงรี
    ต่างกันแค่ แกนตามขวาง "ไม่จำเป็น" ยาวกว่าแกนสังยุค





แกนตามขวางขนานแกน X)

1. สมการไฮเพอร์โบลา

(แกนตามขวางขนานแกน X ค่า A จึงอยู่กับ X)

2. V (h,k)

3. F (h+c, k) F' (h-c, k)

4. A (h+a, k) A' (h-a, k)

5. B (h, k+b) B' (h, k-b)

6. AA' = 2a BB' = 2b

7. latus rectum = 2b²/a

8. directrix x = h + a/e และ x = h - a/e

9. สมการเส้นกำกับ y -k = b/a (x-h) และ y -k = -b/a (x-h)

แกนตามขวางขนานกับแกน Y

1. สมการวงรีคือ

(แกนตามขวาง (a) ขนานแกน Y)

2. V (h,k)

3. F (h, k+c) F' (h, k-c)

4. A (h, k+a) A' (h, k-a)

5. B (h+b, k) B' (h-b, k)

6. AA' = 2a BB' = 2b

7. latus rectum = 2b²/a

8. directrix y = k + a/e และ y = k - a/e

9. สมการเส้นกำกับ x -h = a/b (y-k) และ x-h = -a/b (y-k)

kuza.exteen.com/20071101/entry

------------------------------------------------------------------