ลำดับตอนที่ #2
คืนค่าการตั้งค่าทั้งหมด
คุณแน่ใจว่าต้องการคืนค่าการตั้งค่าทั้งหมด ?
ลำดับตอนที่ #2 : SET เซต
เซต :กลุ่ม หมู่ เหล่า กอง ฝูง ชุดและเมื่อกล่างถึงเซตของสิ่งใด ๆ จะทราบได้ทันทีว่าในเซตนั้นมีอะไรบ้างเราเรียกสิ่งที่อยู่ในเซตว่า สมาชิก
เราไม่สามารถกำหนดเซตของ adj. ได้
เพราะไม่มีมาตรฐานตายตัว เช่น เซตคนหล่อ เซตสาวหื่น เซตคนเก่ง.....
สัญลักษณ์ที่ใช้แทนเซต ชื่อและสมาชิกของเซต
เราไม่สามารถกำหนดเซตของ adj. ได้
เพราะไม่มีมาตรฐานตายตัว เช่น เซตคนหล่อ เซตสาวหื่น เซตคนเก่ง.....
สัญลักษณ์ที่ใช้แทนเซต ชื่อและสมาชิกของเซต
1. สามารถใช้วงกลม, วงรี แทนเซตต่าง ๆ ได้
2. ชื่อเซตนิยมใช้ตัวใหญ่ทั้งหมด เช่น A, B, C, ...
3. สัญลักษณ์แทนคำว่า 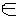 "เป็นสมาชิกของ"
"เป็นสมาชิกของ"
แทนคำว่า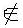 "ไม่เป็นสมาชิกของ
"ไม่เป็นสมาชิกของ
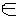 "เป็นสมาชิกของ"
"เป็นสมาชิกของ"แทนคำว่า
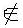 "ไม่เป็นสมาชิกของ
"ไม่เป็นสมาชิกของการเขียนเซตนอกจากจะเขียนวงกลมหรือวงรีล้อมรอบสมาชิกทั้งหมดของเซตแล้วเรายังมีวิธีเขียนเซตได้ 2 วิธี
1) วิธีแจกแจงสมาชิก (Tubular form) มีหลักการเขียน ดังนี้
1. เขียนสมาชิกทั้งหมดในวงเล็บปีกกา
2. สมาชิกแต่ละตัวคั่นด้วยเครื่องหมายจุลภาค (,)
3. สมาชิกที่ซ้ำกันให้เขียนเพียงตัวเดียว
4. ในกรณีที่จำนวนสมาชิกมาก ๆ ให้เขียนสมาชิกอย่างน้อย 3 ตัวแรก แล้วใช้จุด 3 จุด (Tripple dot) แล้วจึงเขียนสมาชิกตัวสุดท้าย
2) วิธีบอกเงื่อนไขของสมาชิก (Set builder form) หลักการเขียนมีดังนี้
1. เขียนเซตด้วยวงเล็บปีกกา
2. กำหนดตัวแปรแทนสมาชิกทั้งหมดตามด้วยเครื่องหมาย | (| อ่านว่า "โดยที")่ แล้ว ตามด้วยเงื่อนไขของตัวแปรนั้น ดังรูปแบบ {x | เงื่อนไขของ x}
เซต | แบบแจกแจงสมาชิก | แบบบอกเงื่อนไข |
A เป็นเซตของจำนวนเต็มบวกที่มีค่าน้อยกว่า 5 | A = {1, 2, 3, 4} | A = {x | x เป็นจำนวนเต็มบวกที่มีค่าน้อยกว่า 5} |
B เซตของวันในหนึ่งสัปดาห์ | B = {วันอาทิตย์, วันจันทร์, วันอังคาร, วันพุธ, วันพฤหัสบดี, วันศุกร์, วันเสาร์} | B = {x | x เป็นชื่อวันในหนึ่งสัปดาห์} |
C เป็นเซตของตัวอักษรในภาษาอังกฤษ | C = {a, b, c, ... ,z} | C = {y | y เป็นตัวอักษรในภาษาอังกฤษ} |
ลักษณะของเซต
เซตว่าง (Empty Set) คือ เซตที่ไม่มีสมาชิกเลย เขียนแทนด้วย { } หรือ
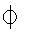 เช่น
เช่น เซตของจำนวนเต็มที่อยู่ระหว่าง 1 กัน 2
เซตของสระในคำว่า "อรวรรณ"
เซตของสระในคำว่า "อรวรรณ"
เซตจำกัด (Finite Set) คือ เซตที่มีจำนวนสมาชิกเท่ากัจำนวนเต็มบวก หรือศูนย์เช่น
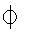 มีจำนวนสมาชิกเป็น 0
มีจำนวนสมาชิกเป็น 0
{1, 2, 3, ...,100} มีจำนวนสมาชิกเป็น 100
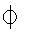 มีจำนวนสมาชิกเป็น 0
มีจำนวนสมาชิกเป็น 0 {1, 2, 3, ...,100} มีจำนวนสมาชิกเป็น 100
เซตอนันต์ (Infinite Set) คือเซตที่ไม่ใช่เซตจำกัด ไม่สามารถบอกจำนวนสมาชิกได้เช่น
เซตของจำนวนเต็มบวก {1, 2, 3, ...}
เซตของจุดบนระนาบ
เซตของจำนวนเต็มบวก {1, 2, 3, ...}
เซตของจุดบนระนาบ
ความสัมพันธ์ของเซต
1. เซตที่เท่ากัน (Equal Sets)
คือ เซตสองเซตที่มีสมาชิกเหมือนกัน
สัญลักษณ์ เซต A เท่ากับ เซต B แทนด้วย A = B
เซต A ไม่เท่ากับ เซต B แทนด้วย A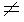 B
B
สัญลักษณ์ เซต A เท่ากับ เซต B แทนด้วย A = B
เซต A ไม่เท่ากับ เซต B แทนด้วย A
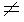 B
BA = {1, 2, 3, 4, 5} B = {1, 2, 3, 4, 3, 2, 5, 5, 5}
เซต A มีสมาชิกเหมือนกับเซต B
A = B
C = {a, e, i, o, u} D = {i, o, u, e, o}
เซต C มีสมาชิกเหมือนกับเซต D
C = D
G = {สีแดง, สีน้ำเงิน, สีขาว} H = {สีแดง, สีน้ำเงิน, สีเหลือง}
สีขาว  G แต่ สีขาว
G แต่ สีขาว  H
H
G 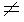 H
H
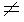 H
H2. เซตที่เทียบเท่ากัน (Equivalentl Sets)คือ เซตที่มีจำนวนสมาชิกเท่ากัน และสมาชิกของเซตจับคู่กันได้พอดีแบบหนึ่งต่อหนึ่ง
สัญลักษณ์ เซต A เทียบเท่ากับ เซต B แทนด้วย A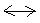 B
B
สัญลักษณ์ เซต A เทียบเท่ากับ เซต B แทนด้วย A
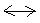 B
BA = {a, b, c, d, e} B = {1, 2, 3, 4, 5}
A 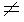 B แต่เซตทั้งสองมีจำนวนสมาชิกเท่ากัน และสามารถจับคู่แบบ 1:1 ได้พอดี
B แต่เซตทั้งสองมีจำนวนสมาชิกเท่ากัน และสามารถจับคู่แบบ 1:1 ได้พอดี
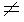 B แต่เซตทั้งสองมีจำนวนสมาชิกเท่ากัน และสามารถจับคู่แบบ 1:1 ได้พอดี
B แต่เซตทั้งสองมีจำนวนสมาชิกเท่ากัน และสามารถจับคู่แบบ 1:1 ได้พอดี A 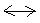 B
B
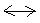 B
BC = {x | x  I+} D = {x | x = 2n , n = 1, 2, 3, ...}
I+} D = {x | x = 2n , n = 1, 2, 3, ...}
C เป็นเซตจำนวนเต็มบวก {1, 2, 3, ...}
ส่วนเซต D เป็นเซตของจำนวนคู่ตั้งแต่ 2 ขึ้นไป {2, 4, 6, ...}
โดยสมาชิกของเซต C กับ D จับคู่แบบ 1:1 ได้พอดี
ส่วนเซต D เป็นเซตของจำนวนคู่ตั้งแต่ 2 ขึ้นไป {2, 4, 6, ...}
โดยสมาชิกของเซต C กับ D จับคู่แบบ 1:1 ได้พอดี
C 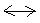 D
D
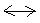 D
Dหมายเหตุ | 1. ถ้า A = B แล้ว A 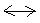 B B2. ถ้า A 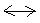 B แล้ว ไม่อาจสรุปได้ว่า A = B B แล้ว ไม่อาจสรุปได้ว่า A = B |
สับเซต
สัญลักษณ์ เซต A เป็นสับเซตของเซต B เเทนด้วย A
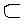 B
Bสัญลักษณ์ เซต A ไม่เป็นสับเซตของเซต B เเทนด้วย A
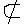 B
BA = {1, 2} B = {2, 3} C = {1, 2, 3} D = {1, 2, 3, 4}
A
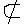 B A
B A 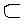 C A
C A 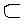 D B
D B 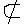 A, B
A, B 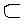 C B
C B 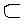 D
D C
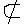 A, C
A, C 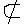 B C
B C 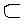 D D
D D 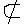 A, D
A, D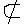 B D
B D 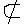 C
C | หมายเหตุ | 1. เซตทุกเซตเป็นสับเซตของตัวมันเอง (A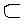 A) A)2. เซตว่าง เป็นสับเซตของทุก ๆเซต ( 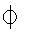 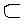 A) A) 3. ถ้า A 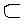 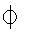 แล้ว A = แล้ว A = 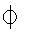 4. ถ้า A 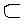 B และ B B และ B 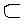 C แล้ว A C แล้ว A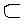 C C5. A = B ก็ต่อเมื่อ A 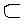 B และ B B และ B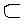 A A |
พาวเวอร์เซต
ถ้า A เป็นเซตใด ๆ เพาเวอร์ของเซต A คือ เซตที่มีสมาชิกเป็นสับเซตทั้งหมดของ A เขียนแทนด้วย P(A)
| เซต A | P(A) |
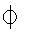 | { 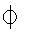 } } |
| {a} | {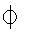 , {a}} , {a}} |
| {a, b} | {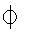 , {a}, {b}, {a, b}} , {a}, {b}, {a, b}} |
| {a, b, c} | {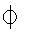 , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}} , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}} |
------------------------------------------------------------------------------------------
แผนภาพของเวนน์-ออยเลอร์
เอกภพสัมพัทธ์ คือ เซตที่กำหนดขอบเขตของสิ่งที่ต้องการศึกษาเขียนแทนด้วย m (ยูนิเวิร์ส)
การพิจารณาเกี่ยวกับเซตจะง่ายขึ้น ถ้าเราใช้แผนภาพของเวนน์-ออยเลอร์ เข้ามาช่วย หลักการเขียนแผนภาพมีดังนี้
1. ใช้รูปสี่เหลี่ยมผืนผ้าหรือสี่เหลี่ยมมุมฉากแทนเอกภพสัมพัทธ์
2. ใช้วงกลมหรือวงรีหรือรูปปิดใด ๆ แทนเซตต่าง ๆ ที่เป็นสมาชิก และเขียนภายในสี่เหลี่ยมผืนผ้า
| 1. | ยูเนียน (Union) | ยูเนียนของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต A หรือ B(เอารวมกัน) เขียนแทนด้วย A 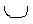 B B |
| 2. | อินเตอร์เซคชัน (Intersection) | อินเตอร์เซคชันของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต A และ B (เอาที่ซ้ำกัน) เขียนแทนด้วย A 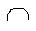 B B |
| 3. | คอมพลีเมนต์ (Complement) | คอมพลีเมนต์ของเซต A คือเซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของเอกภพสัมพัทธ์แต่ไม่เป็นสมาชิกของ A(ไม่เอาเอ) เขียนแทนด้วย A' |
| 4. | ผลต่างของเซต (Difference) | ผลต่างของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต แต่ไม่เป็นสมาชิกขอเซตB(เอาเอไม่ใช่บี ทนด้วย A - B |
| U = {1, 2, 3, ..., 20}, A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10, 12} | |
|---|---|
 A 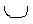 B = {1, 2, 3, 4, 5, 6, 8, 10, 12} B = {1, 2, 3, 4, 5, 6, 8, 10, 12} |  A 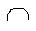 B = {2, 4, 6} B = {2, 4, 6} |
 A' = {7, 8, 9, ..., 20} |  B' = {1, 3, 5, 7, 9, 11, ...,20} |
 (A 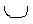 B)' = {7, 9, 11, 13, ..., 20} B)' = {7, 9, 11, 13, ..., 20} |  (A 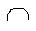 B)' = {1, 3, 5, 7, ..., 20} B)' = {1, 3, 5, 7, ..., 20} |
 A - B = {1, 3, 5} |  B - A = {8, 10, 12} |
จำนวนสมาชิก
ถ้า A เป็นเซตจำกัด เราใช้สัญลักษณ์ n(A) หรือ |A| แทนจำนวนสมาชิกของ A
การหาจำนวนทำได้โดย
1. ใช้แผนภาพ
2. ใช้สูตร
กำหนดให้ Uเป็นเอกภพสัมพัทธ์ A B C เป็นเซตจำกัด
2.1 n(A - B) = n(A) - n(A
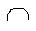 B)
B)2.2 n(B - A) = n(B) - n(B
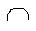 A)
A)2.3 n(A
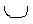 B) = n(A) + n(B) – n(A
B) = n(A) + n(B) – n(A 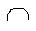 B)
B)2.4 n(A
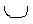 B
B 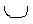 C) =
C) = n(A) + n(B) + n(C) – n(A
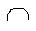 B) – n(A
B) – n(A 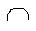 C) – n(B
C) – n(B 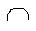 C)+ n(A
C)+ n(A 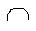 B
B 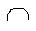 C)
C)สมบัติของเซต
| สัญลักษณ์ | ความหมาย |
| N | เซตของจำนวนนับ |
| I+ | เซตของจำนวนเต็มบวก (จำนวนนับ) |
| I- | เซตของจำนวนเต็มลบ |
| I | เซตของจำนวนเต็ม |
| Q | เซตของจำนวนตรรกยะ |
| Q' | เซตของจำนวนอตรรกยะ |
| R+ | เซตของจำนวนจริงบวก |
| R- | เซตของจำนวนจริงลบ |
| R | เซตของจำนวนจริง |
ข้อมูลจาก...
http://oho.ipst.ac.th/Bookroom/snet2/knowledge_math/set/set9.htm#set9
http://www.tutormaths.com/mathapa1.doc
http://th.wikibooks.org/wiki/%E0%B8%9A%E0%B8%97%E0%B9%80%E0%B8%A3%E0%B8%B5%E0%B8%A2%E0%B8%99%E0%B9%80%E0%B8%8B%E0%B8%95
http://www.nfe.go.th/etv/document/knowledge_mat/knowledge_mat01.pdf
http://www.vcharkarn.com/include/vcafe/showkratoo.php?Pid=81864
http://www.panyathai.or.th/wiki/index.php/%E0%B9%80%E0%B8%8B%E0%B8%95
http://blog.spu.ac.th/malee/2007/12/17/entry-14
เข้าไปทำข้อสอบกันได้(ในบางเว็บ)
--------------------------------------
http://www.tutormaths.com/mathapa1.doc
http://th.wikibooks.org/wiki/%E0%B8%9A%E0%B8%97%E0%B9%80%E0%B8%A3%E0%B8%B5%E0%B8%A2%E0%B8%99%E0%B9%80%E0%B8%8B%E0%B8%95
http://www.nfe.go.th/etv/document/knowledge_mat/knowledge_mat01.pdf
http://www.vcharkarn.com/include/vcafe/showkratoo.php?Pid=81864
http://www.panyathai.or.th/wiki/index.php/%E0%B9%80%E0%B8%8B%E0%B8%95
http://blog.spu.ac.th/malee/2007/12/17/entry-14
เข้าไปทำข้อสอบกันได้(ในบางเว็บ)
เก็บเข้าคอลเล็กชัน



ความคิดเห็น