คืนค่าการตั้งค่าทั้งหมด
คุณแน่ใจว่าต้องการคืนค่าการตั้งค่าทั้งหมด ?
ลำดับตอนที่ #4 : ตรรกศาสตร์ 2
สัจนิรันดร์ ( Tautology)
บทนิยาม สัจนิรันดร์ คือ ประพจน์ที่มีค่าความจริงทุกกรณี
| ตัวอย่างประพจน์ที่เป็นสัจนิรันดร์ที่ควรทราบ มีดังนี้ | ||
| p ∨ ~q | [ ~p ∧ ( p ∨ q)] → q | |
| ~(p ∧ ~q) | [ ( p → q) ∧ ~q ] → ~p | |
| (p ∧ q) → p | (p ∧ q) ⇔ (q ∧ p) | |
| (p ∧ q) → q | (p ∨ q) ⇔ (q ∨ p) | |
| p → (p ∨ q) | (p → q) ⇔ (~p ∨ q) | |
| q → (p ∨ q) | (p → q) ⇔ (~q → ~p) | |
| [ p ∧ ( p → q)] → q | (~p ∨ q) ⇔ (~q → ~p) | |
| [ ~p ∧ ( p → q)] → ~q | ( p ⇔ q) ⇔ [(p → q) ∧ (q → p)] | |
| ข้อสังเกต | ประพจน์ที่สมมูลกัน เมื่อนำมาเชื่อมด้วยตัวเชื่อม ⇔ จะได้ประพจน์ใหม่ซึ่งเป็นสัจนิรันดร์ นั่นคือ ถ้า A และ B สมมูลกันแล้ว A ⇔ B เป็นสัจนิรันดร์ | |
การทดสอบว่าประพจน์ใดเป็นสัจนิรันดร์หรือไม่ ทำได้ 2 วิธีคือ
1. ใช้ตารางค่าความจริง
เพื่อดูว่ามีค่าความจริงเป็นจริงทุกกรณีจริงหรือไม่
2. ใช้การทำ Contradiction
คือการบังคับให้ประพจน์นั้นเป็นเท็จ ถ้าสามารถทำให้ประพจน์นั้นเป็นเท็จได้สำเร็จ แสดงว่าประพจน์นั้นไม่เป็นสัจนิรันดร์ แต่ถ้าไม่สามารถบังคับให้ประพจน์นั้นเป็นเท็จได้ ประพจน์นั้นจะเป็นสัจนิรันดร์ทันที
วิธีทำ
(p
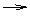 ~q)
~q) 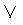 (q
(q 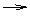 ~p) กำหนดให้มีค่าเป็นเท็จ จะได้
~p) กำหนดให้มีค่าเป็นเท็จ จะได้(p
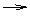 ~q)
~q) 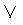 (q
(q 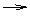 ~p)
~p)F
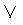 F
Fดังนั้น (p
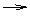 ~q) = F
~q) = F(T
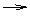 ~T) = F
~T) = F p = T , q = T
(q ~p) = F
(T
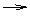 ~T) = F
~T) = F p = T , q = T
ไม่ขัดแย้งกัน แสดงว่าไม่ใช่สัจนิรันดร์
---------------------------------------------------------------------------------------------------
ประโยคเปิด | |||||
| |||||
เราสามารถเขียนแทนประโยคเปิดที่ประกอบด้วยตัวแปร x ด้วยสัญลักษณ์ P(x) หรือ Q(x) และเขียนแทนประโยคเปิดที่ประกอบด้วยตัวแปร x และ y ด้วยสัญลักษณ์ P(x,y) หรือ Q(x,y) | |||||
ตัวอย่างเช่น | |||||
| • เขาเป็นคนดี ⇒ เป็นประโยคเปิดที่ประกอบด้วยตัวแปร “เขา” | |||||
• x > 3 ⇒ เป็นประโยคเปิดที่ประกอบด้วยตัวแปร “x” | |||||
ตัวบ่งปริมาณ | |||||
ตัวบ่งปริมาณ เป็นตัวระบุจำนวนสมาชิกในเอกภพสัมพัทธ์ที่ทำให้ประโยคเปิดกลายเป็นประพจน์ ตัวบ่งปริมาณมี 2 ชนิด คือ | |||||
1. ตัวบ่งปริมาณที่กล่าวถึง “สมาชิกทุกตัวในเอกภพสัมพัทธ์” | |||||
| ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ “∀” อ่านว่า”สำหรับสมาชิก x ทุกตัว” | |||||
2. ตัวบ่งปริมาณที่กล่าวถึง “สมาชิกบางตัวในเอกภพสัมพัทธ์ | |||||
ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ “∃” อ่านว่า “สำหรับสมาชิก x บางตัว” | |||||
ค่าความจริงของประพจน์ที่มีตัวบ่งปริมาณ | |||||
1. ∀x[P(x)] มีค่าความจริงเป็นจริง เมื่อ x ทุกตัวในเอกภพสัมพัทธ์ทำให้ P(x) เป็นจริง | |||||
2. ∀x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อมี x อย่างน้อย 1 ตัวที่ทำให้ P(x) เป็นเท็จ | |||||
3. ∃x[P(x)] มีค่าความจริงเป็นจริง เมื่อมี x อย่าน้อย 1 ตัวที่ทำให้ P(x) เป็นจริง | |||||
4. ∃x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อไม่มี x ใดๆ ในเอกภพสัมพัทธ์ที่ทำให้ P(x) เป็นจริง | |||||
นิเสธของประพจน์ที่มีตัวบ่งปริมาณ | |||||
| ~∀x[P(x)] | สมมูลกับ | ∃x[~P(x)] | |||
| ~∃x[P(x)] | สมมูลกับ | ∀x[~P(x)] | |||
| ~∀x[~P(x)] | สมมูลกับ | ∃x[P(x)] | |||
| ~∃x[~P(x)] | สมมูลกับ | ∀x[P(x)] | |||
| ตัวอย่างเช่น | |||||
• ∀x[x < 0] เมื่อ u = เซตของจำนวนเต็ม | |||||
มีค่าความจริงเป็นเท็จ เพราะเมื่อแทน x เป็นจำนวนเต็มบวกและศูนย์ จะทำให้ x < 0 เป็นเท็จ | |||||
• ∃x[x < 0]เมื่อ u = เซตของจำนวนเต็ม | |||||
มีค่าความจริงเป็นจริง เพราะเมื่อแทน x เป็นจำนวนเต็มลบ จะทำให้ x < 0 เป็นจริง | |||||


ความคิดเห็น