CALCULUS 1

ลำดับตอนที่ #3 : การหาลิมิตของฟังก์ชันที่แบ่งกรณี

การหาลิมิตของฟังก์ชันที่แบ่งกรณี

      ถ้าฟังก์ชันที่โจทย์กำหนดมา มีการแบ่งเป็นหลาย ๆ กรณี โดยฟังก์ชันนั้นถูกแบ่งที่ตำแหน่ง x=a และโจทย์ก็สั่งให้เราหาค่าของ  เราต้องหาแยกลิมิตเป็นสองทางคะ คือหาลิมิตที่ x เข้าใกล้ a ทางลบ(x) และลิมิต x เข้าใกล้ a ทางบวก(x) ค่ะ

      โดยถ้าเมื่อคิดสองทางนั้นแล้วมันได้ค่าผลลัพธ์ที่ออกมาเท่ากัน สรุปได้ว่า ฟังก์ชันก์ f มี
ลิมิตที่ x = a ค๊า

      แต่ถ้าได้ผลลัพธ์ทั้งสองทางไม่เท่ากัน ก็แสดงว่า ฟังก์ชัน f ไม่มีลิมิตที่ x = a เด้อค้า!

 

อ่านไปอ่านมาก็ดูงง ๆ ถ้างั้น เราไปดูตัวอย่างกันเลยดีกว่าเนอะ...

มีตัวอย่างมาให้ดู 2 ข้อค่ะ!
========================================================================


=========================================================================
 
=========================================================================

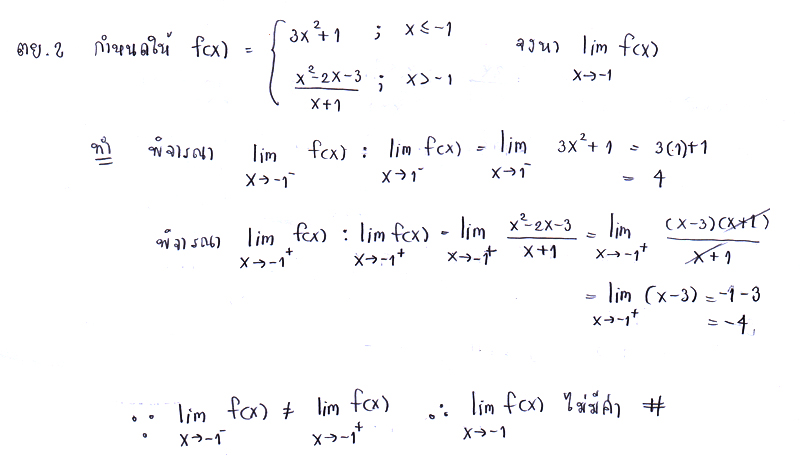
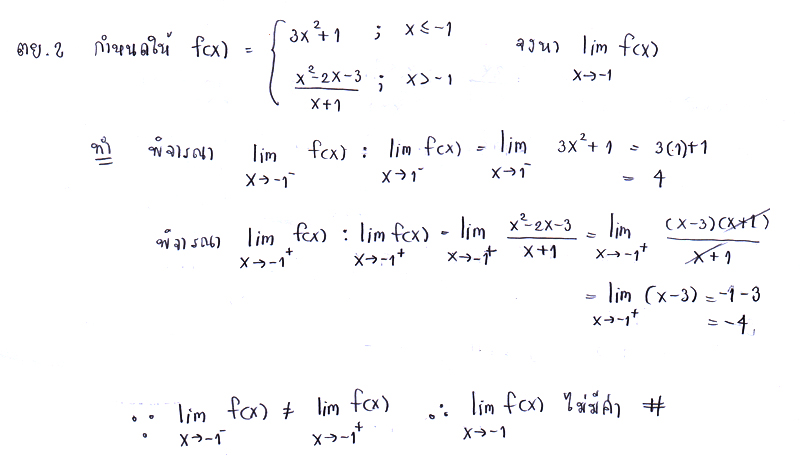
ส่วนแบบฝึกหัดมีทั้งหมด 3 ข้อใหญ่ค่ะ และเนื่องจากว่าพิมพ์ลำบาก ดังนั้นเราขอเขียนละกันนะ ลายมือกากอย่าว่ากัน คริๆ

 

เป็นอย่างไรกันบ้างเอ๋ย พอเข้าใจมั้ย? เห็นป่ะ ว่าพอลองทำความเข้าใจจริง ๆ มันก็ไม่ยากเลย

เลขไม่ได้ยากอย่างที่คุณคิดนะ ^^

ปล. เช่นเคยค่ะ ขอขอบคุณข้อมูลดีดีจากที่ตูน คณะวิทยาศาสตร์ จุฬาฯ ด้วยนะค่ะ(นำมาเขียน

     โดยไม่ได้บอกกล่าวพี่เขาเลยนะ)

    และขอบคุณข้อมูลจากหนังสือแคลคูลัส 1 เล่มสีน้ำเงินด้วยค่า ~!