Pythagoras เิเมื่อ 37 ปี่อนพุทธาลที่เาะ Samos ึ่ั้อยู่ในทะเลนอฝั่เมือ Miletus อรี โลรู้ั Pythagoras ในานะนัิศาสร์บริสุทธิ์ และถ้าเปรียบเทียบ Pythagoras ับนัิศาสร์นอื่นๆ เ่น Euclid และ Archimedes ผู้ึ่โลมีหลัานที่เป็นผลานเียน แ่โลไม่มีลายลัษ์อัษรที่แสว่าเป็นผลานอ Pythagoras เลย ทั้นี้เพราะสัมที่ Pythagoras ใ้ีวิอยู่เป็นสัมที่เร่ศาสนาึ่ถือว่าวามรู้ ือ วามลับ ประเพีเ่นนี้นี่เอที่ทำให้ Pythagoras เป็นบุรุษลึลับไม่เป็นที่รู้ัีเท่า Euclid และ Archimedes
บิาอ Pythagoras เป็นพ่อ้าื่อ Mnesarchus แห่เมือ Tyre และมาราื่อ Phythias แห่เมือ Samos รอบรัวนี้มีลูสามน เมื่อรั้ที่าวเาะ Samos ประสบทุพภิภัย บิาอ Pythagoras ไ้นำ้าวโพไป่วยบรรเทาวามาแลน าวเมือึยย่อให้ Mnesarchus เป็นพลเมือิิมศัิ์ Pythagoras ไ้ใ้ีวิในวัยเ็บนเาะนี้ และมีรูที่เป็นาว Syria สอนวิาารนมีวามสามารถสูทั้ในารเล่นพิ แ่บทวี และท่อบทประพันธ์อ Homer ไ้อย่าึ้นใ
อนึ่ Pythagoras อามีรูสอนวิทยาารแนอื่นๆ อีหลายน แ่รูที่มีอิทธิพล่อวามนึิอ Pythagoras มาที่สุือ Thales แห่เมือ Miletus และศิษย์เออ Thales ที่ื่อ Anaximander เมื่ออายุ 18 ปี Pythagoras ไ้เินทาไป Miletus เพื่อพบ Thales ผู้รา ารไ้เรียนหนัสือับ Thales ทำให้ Pythagoras รู้สึสนใิศาสร์ ับ าราศาสร์มา ึเินทาไปศึษาวิาทั้สอนี้่อที่อียิป์ ามำแนะนำอ Thales ประวบับะนั้นษัริย์ Polycrates ผู้ทรปรอเาะ Samos ทรเป็นษัริย์ที่โหเหี้ยมและทารุมา ารเินทาออนอประเทศไปอียิป์ ึทำให้ Pythagoras รู้สึปลอภัยและยินี
ะพำนัอยู่ในอียิป์ Pythagoras ทำนเสมือนเป็นาวอียิป์ เ่น ไปศาสนสถานศัิ์สิทธิ์เพื่อนสนทนาับบรรานับว ไม่บริโภพืประเภทถั่ว ไม่นุ่ห่มเสื้อผ้าที่ทำาหนัสัว์ ฯลฯ และเมื่ออ์ษัริย์ Cambyses ที่ 2 แห่อาาัรเปอร์เียทรรุรานอียิป์ โยไ้เ้ายึเมือ Heliopolis ับเมือ Memphis ทหารอษัริย์ Cambyses ที่ 2 ไ้ับ Pythagoras เป็นเลยสราม และนำัวไปัที่รุ Babylon น Pythagoras อายุ 23 ปี ็ถูปล่อยเป็นไท เพราะษัริย์ Cambyses ทร่าัวาย Pythagoras ึเินทาลับ Samos ึ่ะนั้นอยู่ใ้ารปรออัรพรริ Darius แห่ Persia แล้วไ้เินทา่อไปที่เาะ Crete เพื่อศึษาหมาย เมื่อสำเร็ารศึษา็เินทาลับ Samos เพื่อั้สถาบันารศึษาที่เรียว่า semicircle ให้าวเาะที่สนใมาพบปะสนทนาารเมือและริยธรรม วามีามรวมถึวามยุิธรรม้วย
เมื่ออายุ 35 ปี Pythagoras ไ้เินทาไปเมือ Crotone ึ่ั้อยู่ทาอนใ้ออิาลี เพราะที่นั่น ะนั้นเป็นเมือึ้นอรี และรับาลรีไ้ัั้โรเรียนสอนศาสนาและปรัาให้แ่าวเมือ Pythagoras ึมีสานุศิษย์หลายน และศิษย์ทุน่า็บำเพ็นเสมือนเป็นนัพร เ่น ินอาหารมัสวิรัิ ไม่นิยมมีทรัพย์สมบัิและมีวามเื่อแปลๆ เ่น ไม่ให้นนาแอ่นมาทำรับนหลัาบ้าน เป็น้น นอานี้ผู้น็ยัเื่อาม Pythagoras อีว่า ธรรมาิับิศาสร์มีวามเี่ยว้อัน และำนวนเลมีวามสำั ือ มีัวน เ่น เรือ 2 ลำ ับเรือ 3 ลำ รวมเป็น 5 ลำ หรือถ้าะพูเินามธรรมว่า 2 + 3 = 5 ็เป็นริทุรี ไม่ว่าสิ่ที่นับเป็น ้า ม้า หรือเ้าอี้ ฯลฯ ้วยเหุนี้ำนวน 2, 3 ึมีัวน เหมือนปาา หรือเรือ ันั้น ในมุมมออ Pythagoras ำนวนเลทุำนวนมีบุลิภาพ ือ สมบูร์ หรือบพร่อ สวย หรือน่าเลีย ู่ หรือี่ เป็น้น
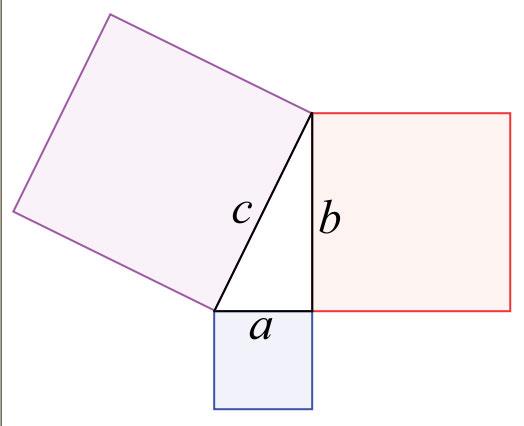
ทุวันนี้เราทุนรู้ัทฤษีสามเหลี่ยมมุมาที่ว่า a² = b² + c² อ Pythagoras เมื่อ a ือ ้านร้ามมุมา และ b ับ c เป็น้านประอบมุมา ถึาว Babylon ะรู้ทฤษีนี้เมื่อ 1,000 ปี่อน็าม แ่ Pythagoras อาเป็นนัิศาสร์นแรที่พิสูน์ทฤษีนี้ไ้ และำนาน็เล่าว่า เมื่อเาพบสมารนี้เาไ้่าวัว เพื่อถวายเป็นพลีแ่พระเ้า
นอาทฤษีที่โ่ันี้แล้ว Pythagoras ็ยัมีผลานอื่นอี เ่น
1) ารไ้พบว่า ผลบวมุมภายในอสามเหลี่ยมใๆ ะเท่าับ 2 มุมาเสมอ และในรีรูป n เหลี่ยม ผลบวอมุมภายใน = (2n - 4) มุมา ส่วนผลบวอมุมภายนอ = 2 มุมาเสมอ
2) สามารถแ้สมาร (a – x) = x² ไ้โยใ้วิธีเราิ
3) เป็นปรา์นแรที่เสนอวามิว่าโลลม โยไ้้อสรุปนี้ าารเห็นเาอโลที่ทาบบนวันทร์ในปราาร์ันทรุปราาว่ามีลัษะโ้เสมอ นอานี้ Pythagoras ็ยัรู้อีว่าระนาบโรอวันทร์อโลเอียทำมุมเล็ๆ ับแนวเส้นศูนย์สูรอโล
4) เป็นบุลแรที่พบว่า าวประายพฤษ์ และาวประำเมือ ือ าววเียวัน
5) เสนอวามิว่าโล ือ ุศูนย์ลาอเอภพที่ถูห่อหุ้ม้วยทรลมใสมามาย และทรลมมีาวฤษ์ิอยู่ที่ผิว โยทุทรลมะหมุนอย่า้าๆ รอบโล้วยวามเร็วสม่ำเสมอ
เมื่ออายุ 35 ปี สมาม Pythagoras ถูนเผ่า Cylon โมี Pythagoras ึ้อหนีไปเมือ Metapontium และเสียีวิที่นั่นเมื่อ พ.ศ. 43 สิริอายุไ้ 80ปี
ัไ้ล่าวมาแล้วว่า ทฤษี Pythagoras เป็นทฤษีิศาสร์ที่นัเรียนทุนรู้วิธีพิสูน์ ถึระนั้น หนัสือ The Pythagorean Proposition อ Elisha S. Loomis ็ไ้แสวิธีพิสูน์ทฤษีนี้บทนี้ถึ 367 วิธี โยไ้พิสูน์แบบพีิ 109 วิธี และพิสูน์แบบเราิ 235 วิธี และวิธีอื่นๆ อี
เ่น ถ้าพิาราสามเหลี่ยมมุมา RST ที่มี RT เป็น้านร้ามมุมา และลาเส้น SD ให้ั้าับ RT ที่ D เพราะสามเหลี่ยม RSD มีพื้นที่ ½a² cosθ sinθ
เมื่อ a ือ วามยาวอ้าน RS และ θ ือ มุม TRS
ในทำนอเียวันเรา็ะไ้ว่า
สามเหลี่ยม SDT มีพื้นที่ ½b² cosθ sinθ และสามเหลี่ยม RST มีพื้นที่ ½ c²cosθ sinθ ้วย แ่พื้นที่สามเหลี่ยม RST = พ.ท.สามเหลี่ยม RSD + พ.ท. สามเหลี่ยม SDT
ันั้น c² = a² + b²
ผลระทบหนึ่ที่เิาารใ้ทฤษีนี้ ือ ถ้าบน้าน a, b, c อสามเหลี่ยมมุมา แทนที่ะสร้ารูปสี่เหลี่ยมัุรัส Loomis ไ้สร้ารูปอะไร็ไ้ โยให้้านๆ หนึ่อรูปนั้น เป็นเส้นรที่ยาว a, b และ c และให้รูปทั้สามมีนาที่เป็นปิภาโยรับวามยาวอ้าน a, b, c
เมื่อให้ Fa, Fb และ Fc ือ พื้นที่อรูปทั้ 3
เพราะ พ.ท. Fa = Ka² าวามริที่ว่าพื้นที่แปรโยรับวามยาวยำลัสอ
ันั้น พ.ท. Fb = Kb²
และ พ.ท. Fc = Kc²
าทฤษี Pythagoras ที่ว่า a² + b² = c²
แสว่า Ka² + Kb² = Kc²
นั่นือ Fa + Fb = Fc
หนัสือเล่มนี้ยัไ้เสนอวิธี้นหาุอำนวนเลที่มีสมบัิามทฤษีอ Pythagoras ้วยว่าถ้าให้
x = a² – b²
y = 2ab
z = a² + b²
แล้ว x² + y² ะเท่าับ z² เสมอ ไม่ว่า a, b ะเป็นำนวนเ็มใ็าม เ่น ถ้าให้ a = 7, b = 4 เราะไ้
x = 49 – 16 = 33
y = 2 × 4 × 7 = 56
z = 49 + 16 = 65
นั่นือ 33²+ 56² = 65² ันั้น a, b ในที่นี้ึถูเรียเป็นำนวนำเนิ
สมบัิอื่นๆ ที่น่าสนใอสามเหลี่ยมมุมามีมามาย เ่น ในรีสามเหลี่ยมมุมาที่มี้านยาว 6, 8, 10 ับ 5, 12, 13 เรา็ะพบว่าสามเหลี่ยมทั้สอรูปนี้มีเส้นรอบรูปยาวเท่าับพื้นที่พอี ือ 24 ับ 30
ส่วน Fermat ในปี .ศ. 1643 ็ไ้พบว่า ถ้าให้้านร้ามมุมาเป็นำลัสอสมบูร์แล้ว้านที่ประอบมุมารวมัน ะเป็นำลัสอสมบูร์้วย และรูปสามเหลี่ยมมุมาที่ให่ที่สุ มี้านทั้สามยาว 4,565,486,027,761 ับ 1,061,652,293,520 และ 4,657,298,610,289
ในรีสามเหลี่ยมมุมาที่มี้านประอบมุมายาว 693 ับ 1924 และ้านร้ามมุมายาว 2045 เรา็ะไ้ว่า สามเหลี่ยมนี้มีพื้นที่ 666,666
ถึโยทั่วไปสามเหลี่ยมหน้าั่วะไม่เป็นสามเหลี่ยมมุมา แ่ถ้าะให้ใล้เียที่สุ สามเหลี่ยมหน้าั่วนั้น็ะมี้านๆ หนึ่ยาว 21, 669, 693, 148, 613, 788, 330, 547, 979, 729, 286, 307, 164, 015, 202, 768, 699, 465, 346, 081, 691, 992, 338, 845, 992, 696 ส่วน้านที่ร้ามมุมา็ะยาวเท่าับ้านๆ หนึ่ +1
นอานี้เรา็ยัพบอีว่า มีสามเหลี่ยมมุมา สามรูป ือ (1) (1380 ; 19,019 : 19,069) (2) (3,059 ; 8,580 : 9109) และ (3) (4,485 ; 5,852 : 7373) ที่มีพื้นที่เท่าัน ือ 13,123,110 ำถามมี่อว่า มีสามเหลี่ยมมุมาอื่นใอีที่มีพื้นที่ 13,123,110
ถ้าำหนำนวนเ็มมาให้ำนวนหนึ่ ำถามมีว่าำนวนนี้ ือ พื้นที่อสามเหลี่ยมมุมาที่มี้านทั้สามเป็นำนวนรรยะ หรือไม่
ยัวอย่าำนวนเ็ม 6 นี่ือ พื้นที่อรูปสามเหลี่ยมมุมาที่มี้านยาว 3, 4, 5 และสำหรับำนวนเ็ม 5 นั้น นี่็ือ พื้นที่อรูปสามเหลี่ยมมุมาที่มี้านยาว 3/2, 20/3 และ 41/6
สำหรับ 1, 2, 3, 4 นั้นไม่ใ่พื้นที่อรูปสามเหลี่ยมมุมาที่วามยาวอ้านทั้สามเป็นำนวนรรยะเลย
ันั้น โทย์ยา ือ ถ้าำหนพื้นที่ N อสามเหลี่ยมมุมามาให้ ึ่ N เป็นำนวนเ็ม หา้านทั้สามที่เป็นำนวนรรยะอสามเหลี่ยมมุมานั้น
ในารอบโทย์้อนี้ นัิศาสร์้านทฤษีำนวน ไ้รู้มานานแล้วว่า
ำอบะหาไ้าารแ้สมาร y² = x³ - N²x ึ่ถ้า a, b เป็น้านประอบมุมา และ c เป็น้านร้ามมุมา เราะไ้ x =(c/2)² และ y = (a² - b²)c/8
เ่นในรี N = 6 ้านที่ยาว 3, 4, 5 ือ a = 4, b = 3 และ c = 5 นั้น ะให้ x = 25/4 และ y = 35/8 เป็นำอบอสมาร y² = x³ - 36x
แ่นระทั่วันนี้ นัิศาสร์็ยัไม่มีสูรทั่วไปที่ใ้ในารัสินว่า สมาร y² = x³ - N²x ะมีำอบอ x ับ y ที่เป็นำนวนรรยะหรือไม่ เมื่อำหน่า N ที่เป็นำนวนเ็มมาให้
ถ้ามีใรรู้ำอบนี้ Pythagoras เอ ็รู้สึเป็นสุ้วย
สุทัศน์ ยส้าน เมธีวิัยอาวุโส สว.
|




ความคิดเห็น