ค่าเริ่มต้น
- เลื่อนอัตโนมัติ
- ฟอนต์ THSarabunNew
- ฟอนต์ Sarabun
- ฟอนต์ Mali
- ฟอนต์ Trirong
- ฟอนต์ Maitree
- ฟอนต์ Taviraj
- ฟอนต์ Kodchasan
- ฟอนต์ ChakraPetch
คืนค่าการตั้งค่าทั้งหมด
คุณแน่ใจว่าต้องการคืนค่าการตั้งค่าทั้งหมด ?
ลำดับตอนที่ #4 : การหาแรงลัพธ์ โดยวิธีคำนวณ
• วิธีที่ 1 ใช้การแตกแรงหรือแยกแรง •
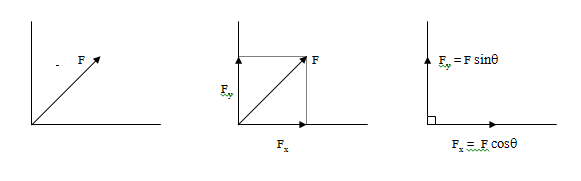
การแตกแรงหรือแยกแรง คือการแยกแรง 1 แรงออกเป็นแรงองค์ประกอบ 2 แรงซึ่งตั้งฉากกันอยู่ตามแนวแกน x และแกน y
F เป็นขนาดของแรงที่มี F ทำมุม q กับแกนนอนหรือแกน x
Fx เป็นขนาดของแรงตามแนวแกน x
Fy เป็นขนาดของแรงตามแนวแกน y
________________________________________________
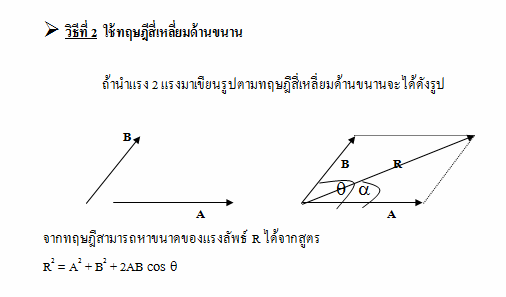
• วิธีที่ 2 ใช้ทฤษฎีสี่เหลี่ยมด้านขนาน •
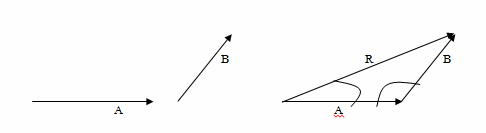
ถ้านำแรง 2 แรงมาเขียนรูปตามทฤษฎีสี่เหลี่ยมด้านขนานจะได้ดังรูป
พิสูจน์สูตร จากรูป X = B sin q
Y = B cos q
ตามรูป และ Pythagorus ( รูปสามเหลี่ยมมุมฉาก , รูปใหญ่ )
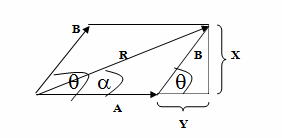
R2 = (A + Y)2 + X2
= (A + B cos q)2 + (B sin q)2
= A2 + 2AB cos q + B2 cos2 q + B2 sin2 q
= A2 + 2AB cos q + B2 ( sin2 q + cos2 q )
จากตรีโกณ sin2 q + cos2 q = 1 ดังนั้นจะได้ว่า
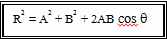
และหาทิศของ R หรือมุม a ได้จากสูตร
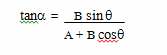
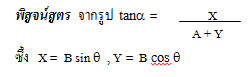
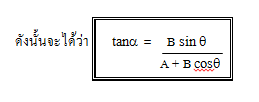
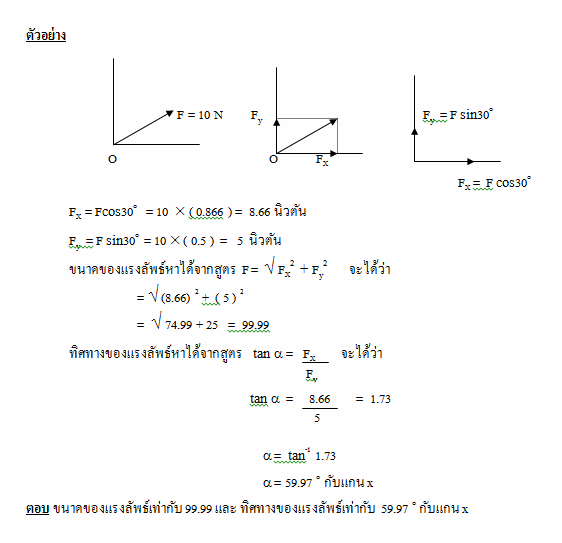
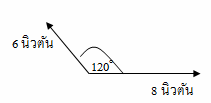
ตัวอย่าง มีแรง 2 แรงขนาด 8 นิวตัน และ 6 นิวตัน โดยทำมุม 120๐ กับจุด O ดังรูป จงหาขนาดและทิศทางของแรงลัพธ์
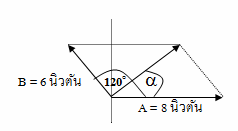
วิธีทำ หาขนาดและทิศทางของแรงลัพธ์โดยใช้ทฤษฎีสี่เหลี่มด้านขนาน จะได้รูป
จากสูตร R2 = A2 + B2 + 2AB cos q
R2 = ( 8 )2 + ( 6 )2 + 2(8)(6) cos 120๐
= 64 + 36 + 96 cos (180๐- 60๐)
= 100 + 96 (- cos 60๐)
= 100 – (96 )(0.5)
R2 = 100 – 48 = 52
R = √ 52 = 7.2 นิวตัน
ตอบ ขนาดของแรงลัพธ์เท่ากับ 7.2 นิวตัน และมีทิศทางทำมุม 45.8 ๐ กับแกน x
_________________________________________________
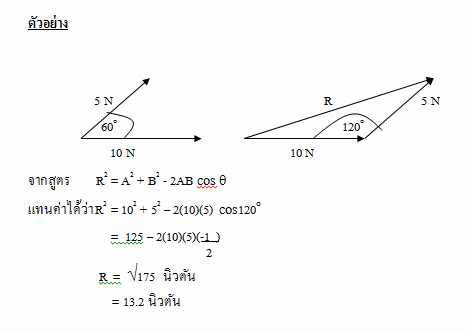
• วิธีที่ 3 ใช้กฎของ cos •
จากกฎของ cos สามารถหาขนาดหรือความยาวของ R ได้เท่านั้น
การใช้กฎของ cos เราใช้ด้านตรงข้ามมุม และใช้สูตรเป็น -
ซึ่งจะใช้สูตร R2 = A2 + B2 - 2AB cos q ( q คือมุมภายในสามเหลี่ยมและอยู่ตรงข้ามกับ R)
_________________________________________________
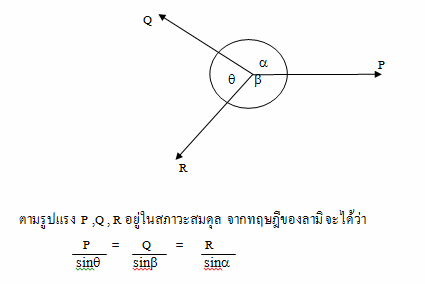
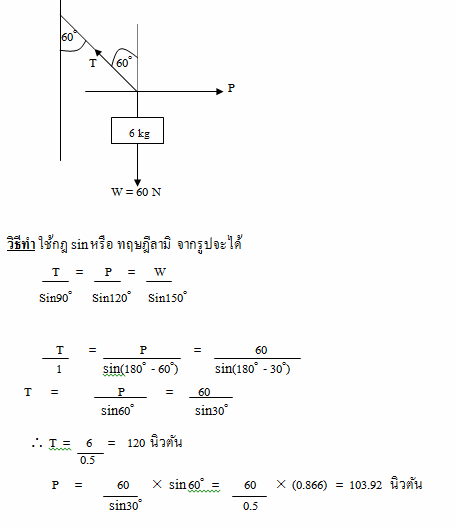
• วิธีที่ 4 ใช้กฎ sin หรือ ทฤษฎีลามิ ( Lami Theorem ) •
เมื่อมีแรงสามแรงมากระทำต่อวัตถุร่วมกันที่จุด ๆหนึ่ง และอยู่ในสภาวะสมดุล จะได้ว่า อัตราส่วน
บทแทรกของทฤษฎีของลามิ กล่าวว่า เมื่อมี 3 แรงมากระทำร่วมกันที่วัตถุหนึ่งแล้วทำให้วัตถุอยู่ในสภาวะสมดุล รูปสามเหลี่ยมใดก็ตามที่มีด้านทั้งสามตั้งฉากกับแนวของแรงทั้งสามนั้นตามลำดับแล้วด้านทั้งสาม ของรูปสามเหลี่ยมนั้น ย่อมเป็นสัดส่วนโดยตรงกับแรงซึ่งมีแนวตั้งฉากกับด้านนั้นตามลำดับ
ตัวอย่าง เชือกเส้นหนึ่งผูกวัตถุมวล 6 กิโลกรัม ปลายอีกข้างหนึ่งตรึงติดกับฝาผนัง ออกแรงดึงวัตถุไปในแนวระดับด้วยแรง P ทำให้เส้นเชือกเอียงทำมุม 60 ๐ กับฝาผนัง จงหาแรงตึงของเชือกและแรง P ที่ใช้ดึง
ตอบ แรงตึงเชือก T เท่ากับ 120 นิวตัน และแรง P ที่ดึงเท่ากับ 103.92 นิวตัน
ทบทวน จากคณิตศาสตร์
- sin(A ± B) = sinAcosB ± cosAsinB - cos(A ± B) = cosAcosB + sinAsinB
_________________________________________________
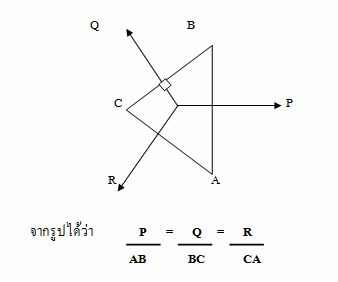
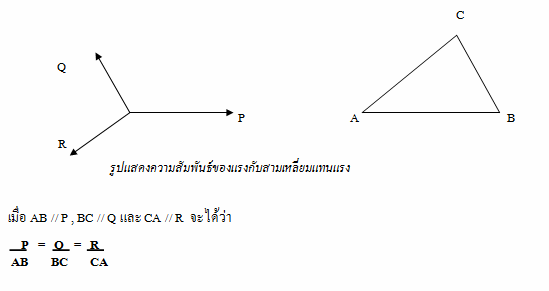
• วิธีที่ 5 ใช้ทฤษฎีสามเหลี่ยมแทนแรง •
กล่าวว่า ถ้ามีแรงสามแรงมากระทำร่วมกันที่จุดๆหนึ่ง และแรงทั้งสามแรงอยู่ในสภาวะสมดุล ขนาดและทิศทางของแรงทั้งสามสามารถแทนได้โดยด้านทั้งสามของสามเหลี่ยมรูปหนึ่ง เมื่อด้านทั้งสามของรูปสามเหลี่ยมนั้นขนานกับแนวแรงทั้งสามตามลำดับ
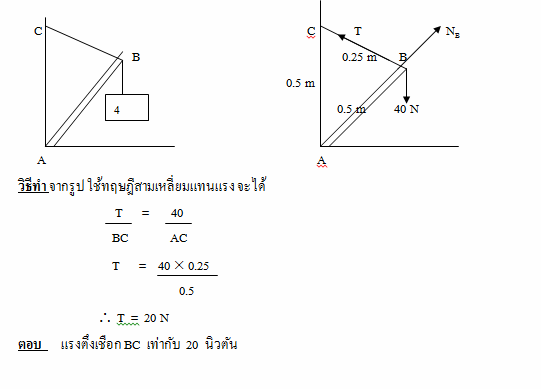
ตัวอย่าง คาน AB ยาว 0.5 เมตร เสียบอยู่กับซอกกำแพงที่จุด A ที่ปลาย B มีเชือก BC ผูกติดกับกำแพงที่จุด C โดยBC ยาว 2.5 เมตร และ AC ยาว 0.5 เมตร นำก้อนน้ำหนัก 4 กิโลกรัม ผูกติดที่ปลาย B ดังรูป จงหาแรงตึงเชือก BC
_________________________________________________
ก่อนจากกัน*









3ความคิดเห็น